2020-05-11
380
При пересечении лучи не влияют друг на друга и распространяются независимо друг от друга. Он выполняется при небольших интенсивностях света и нарушается при сильном лазерном излучении.
Первые два закона вытекают из принципа Ферма: (Пьер, 20.08.1601г.-12.01.1665г.) французский математик и физик.
Свет распространяется таким путем, для прохождения которого ему требуется минимальное время.
| S |
| 2 |
| 1 |
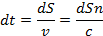
Тогда время прохождения луча из т.1 в т.2
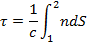
величина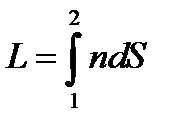 
- оптическая длина пути
Свет распространяется таким образом, чтобы оптическая длина пути была минимальною.
Из принципа Ферма вытекает обратимость световых лучей, то есть
Луч, который был пущен из т. 2 в т. 1, распространяется по той же траектории, что и луч, идущий из т.1 в т.2, только в обратном направлении.
| d |
| γ |
| S |
| C |
| b |
| β |
| α |
| α |
| x |
| a |
| Xx |
| рис |
| Y |
| n1 |
| n2 |
| yx |
| γпр |
| S |
| C |
| αпр |
| Xx |
| рис |
| Y |
| n1 |
| n2 |
Получим с помощью принципа Ферма закон отражения света.
. 
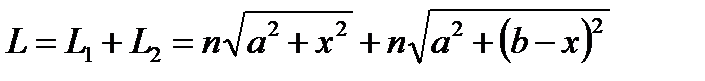
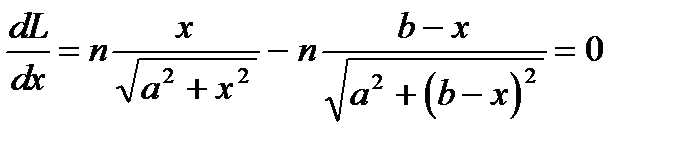
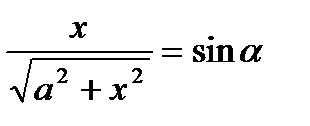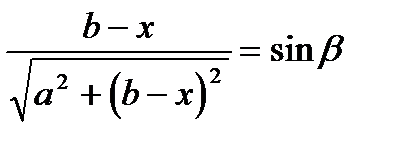откуда 
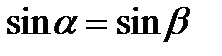или α=β
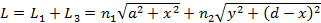
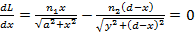
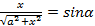
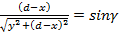откуда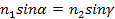 
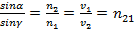
При переходе света из оптически более плотной среды в оптически менее плотную при некотором предельном угле падения α пр = arcsin n 21 угол преломления γпр оказывается равным π/2. Таким образом, при α пр <α <π/2 наблюдается непрохождение луча во вторую среду, а его полное внутреннее отражение в первую среду.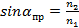 
для воздуха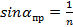 
Данное явление используется, например, в световодах, в оптических приборах для поворота лучей и изображения.
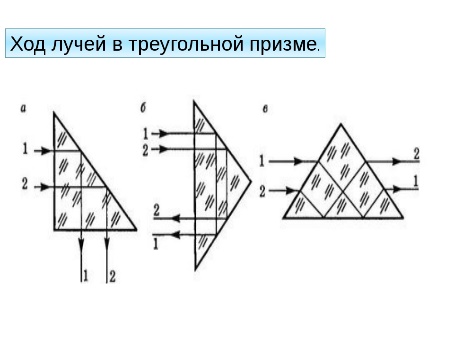
Ход лучей в призме.
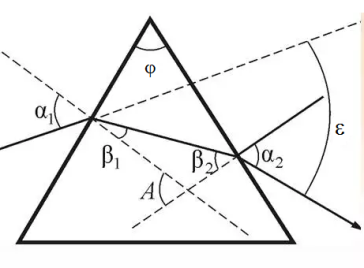
Рассмотрим ход луча монохроматического (одной частоты или длины волны) света
n2>n1
j - преломляющий угол, e - отклоняющий угол
Определим ε в зависимости от φ и n.
| γ |
| ε |
| φM |
| α |
Из рисунка видим, что
a = j g = j + e
так как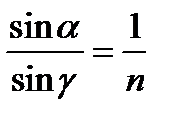 
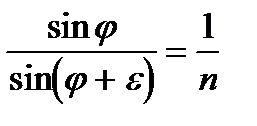
то sin(φ +ε)=n sin φ
при малых φ j + e=nφ, или e = (n-1) φ
Если луч падает на вторую грань α>αпр, то он полностью отразится. В этом случае призмы можно использовать вместо зеркал. Для стекла-воздух
aпр=arcsin(1/1,5)=450
Линзы
Линзой (лат. lens – чечевица) называется прозрачное тело, ограниченное двумя сферическими поверхностями (одна поверхность может быть плоской) и преобразующее форму светового пучка. Линзы подразделяются на
двояковыпуклые (рис. 3.3, 1), двояковогнутые (4), плосковыпуклые (2),
плосковогнутые (5), выпукло-вогнутые (3) и вогнуто-выпуклые (6).
Собирающие линзы – линзы, превращающие входящие параллельные пучки в пучок сходящихся лучей Условное обозначение собирающей линзы (
). (на рис. 3.3, линзы 1, 2, 3).
Рассеивающие линзы – линзы, превращающие входящие параллельные пучки в пучки расходящихся лучей Условное обозначение рассеивающей линзы(на рис. 3.3, линзы 4, 5, 6).
Тонкая линза – линза, у которой радиусы кривизны ограничивающих поверхностей намного больше толщины линзы
.
Главная оптическая ось – прямая, проходящая через центры О1, О2
ограничивающих сферических поверхностей линзы.
Оптический центр – точка 0, расположенная на главной оптической оси
O1О2, проходя через которую луч света не изменяет своего направления.
27
Побочная оптическая ось – произвольная прямая MN, проходящая
через оптический центр линзы 0 под углом к главной оптической оси.
Множество прямых, проходящих через цёнтр линзы 0, составляет множество
побочных оптических осей.
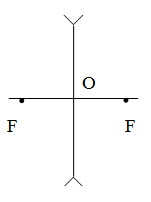
Главный фокус – точка F на главной оптической оси, в которой пересекаются преломленные линзой сходящиеся лучи, падающие на линзу параллельно главной оптической оси. Линза имеет два главных фокуса F.
Фокальная плоскость – плоскость РN, проходящая через главный фокус линзы перпендикулярно главной оптической оси. Фокальная плоскость состоит из бесконечного множества побочных фокусов линзы.
Побочный фокус – точка N фокальной плоскости, в сов линзы.
Фокусное расстояние линзы F – расстояние от центра линзы 0 до
главного фокуса F – отрезок 0F.
