Теорема Гаусса для электрического поля

Здесь ничего не изменится, если полагать, что заряды меняются с течением времени. Т.е. уравнения электростатики, остаются без изменений

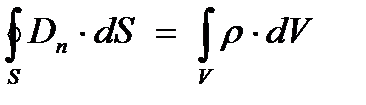 - это одно из уравнений Максвелла в интегральной форме ‑ поток вектора электрической индукции через замкнутую поверхность равен сумме зарядов внутри этой поверхности.

Для произвольного вектора  справедлива Остроградского:

,

где  

Тогда

Ему соответствует уравнение в дифференциальной форме: .

Дивергенция вектора электрической индукции  равна плотности электрических зарядов .

К этим уравнениям добавляют, так называемое, уравнение среды:

.

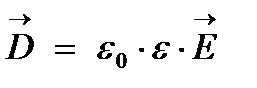Вектор электрической индукции 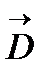 равен произведению электрической постоянной ε₀ на диэлектрическую проницаемость среды  и на вектор напряженности электрического поля .

Кроме того, к этому уравнению среды добавляют еще одно уравнение среды, являющееся законом Ома в дифференциальной форме:

Вектор плотности тока 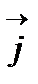 равен произведению электропроводности среды  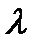 на вектор напряженности электрического поля .

Теорема Гаусса для магнитного поля

Эта теорема отражает тот факт, что в природе нет магнитных зарядов. Она без изменений переходит в систему уравнений Максвелла.

Уравнение Максвелла в интегральной форме ‑ поток вектора магнитной индукции  через замкнутую поверхность равен нулю.

Аналогично, существует дифференциальная форма этого уравнения: . Дивергенция вектора магнитной индукции 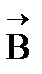 равна нулю.

К этим уравнениям также добавляется уравнение среды: = Вектор магнитной индукции  равен произведению магнитной постоянной μ₀, на магнитную проницаемость среды μ и на вектор напряженности магнитного поля .