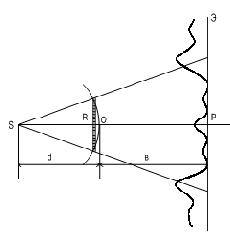
Рассмотрим сферическую волну, распространяющуюся от точечного источника S, на пути которой находится непрозрачный диск.
| b |
| Экран |
| P |
| S |
| b+mλ/2 |
| рис |
Амплитуда световых колебаний в точке P равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке P будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).
В этом случае участки, закрытые диском, надо исключить из рассматривания
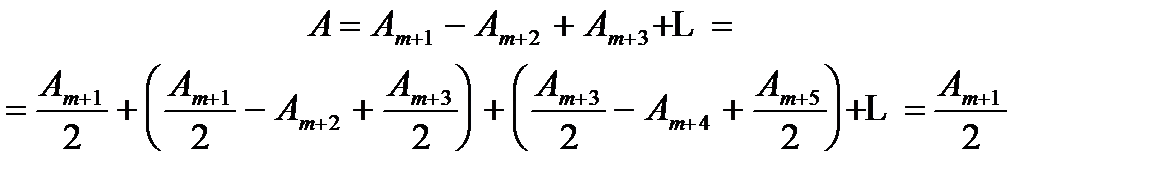
 то есть
то есть 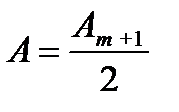 .
.
Таким образом, в центре всегда наблюдается интерференционный максимум, соответствующий первой половине амплитуды первой открытой зоны Френеля. Центральный максимум, окруженный концентрическими с ним чередующимися темными и светлыми интерференционными кольцами. С увеличением радиуса диска первая открытая зона удаляется от центра и, что особенно важно, увеличивает угол (между нормалью к поверхности и направлением на точку наблюдения. Поэтому интенсивность центрального max ослабляется. Если радиус диска на много больше, чем радиус закрываемой им центральной зоны Френеля, то есть перекрывает много зон, в этом случае Ам+1<<А1, и позади диска наблюдается обычная тень, а экрану для выбора элемента поблизости границы имеется очень слабая интервенционная картина. В том случае возможно пренебречь явлением дифракции и выполняются законы прямолинейного распространения света.
В 1818г. Парижская академия наук предложила дифракцию света в качестве работы на премию. Френель представил волновую теорию дифракции, в которой Пуассон увидел противоречие: за непрозрачным диском должно наблюдаться светлое пятно. Опыт, проведённый Араго, подтвердил наличие такого пятна, которое впоследствии было названо «Пятном Пуассона». Оно подтверждает правильность теории Френеля.
 2020-05-11
2020-05-11 169
169








