Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
^ - обозначила степень, потому что степень в степени изобразить не получается, а скобками () обозначила то, что в степень возводится. Смотрите внимательно!!!
Р (а  Х
Х  b) =
b) =  =
= 
 ((x-m)^2)/2(σ^2) dx
((x-m)^2)/2(σ^2) dx
Обозначим
 = t,
= t,  = α,
= α,  = β
= β
Тогда Р(а  ) =
) = 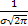
 –(t^2) σ
–(t^2) σ  dt =
dt = 
 –(t^2) dt =
–(t^2) dt =  [ Ф(β) – Ф(α)]
[ Ф(β) – Ф(α)]
Так как интеграл  -(t^2) dt не выражается через элементарные функции, то вводится в рассмотрение функция
-(t^2) dt не выражается через элементарные функции, то вводится в рассмотрение функция
Ф(х) = 
 –(t^2) dt,
–(t^2) dt,
которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х подсчитаны и приводятся в специальных таблицах.
Функция Лапласа обладает следующими свойствами:
1. Ф(0) = 0
2. Ф (-х) = -Ф(х)
3. Ф(¥) = 1
Функцию Лапласа называют также функцией ошибок и обозначают erf x.
Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
 (х)=
(х)=  Ф(
Ф(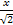 ) =
) = 
 –(t^2)/2 dt.
–(t^2)/2 dt.
 2020-05-21
2020-05-21 169
169








