Числовые характеристики случайных величин, распределенных по равномерному, показательному и нормальному законам (значения мат. ожидания и дисперсии)

1.Равномерное распределение

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения (^ - местами, где не получилось сделать верхний индекс, этим знаком обозначена степень)

                                                                        b

MX =     =   =  | =   

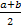
                                                                       a b

MX²  =   =    = | =    =

                                                                            a

 

DX = MX² – (MX)²  =   -   =   =

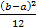
Среднее квадратическое отклонение

σX =   =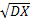

 

2.Показательное распределение

Найдем математическое ожидание и дисперсию.

                                                                                                                               ∞

MX =    = dx =   = λ(-   |  +  dx = 

                                                                                                                                ⁰

                                 ∞

-    | =

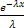                                 0

Результат получен с использованием того факта, что

    ∞

xe^-λx  | = 0

    0

Для нахождения дисперсии найдем величину MX²

MX² =   =

Дважды интегрируя по частям получаем

MX² =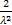

 

 Тогда DX = MX² – (MX)²  =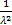

σX =

 

3.Нормальное распределение

Найдем математическое ожидание и дисперсию.

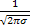
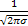
MX =   = *()dx =

z = (x-a)/σ

Поскольку   как интеграл по всей прямой от нечетной функции.

Таким образом, параметр а – математическое ожидание.

Найдем дисперсию нормальной случайной величины, снова применяя замену z = (x-a)/σ и интегрируя по частям:

DX = M(X-MX)² =  =   =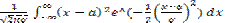

                                                                   ∞

 =    +

σ²  - это дисперсия, а σ – среднее квадратичное отклонение.

 

 

Что такое совместная плотность распределения непрерывной двумерной случайной величины? Укажите ее свойства. Как построить по плотности совместного распределения плотности распределения и функции распределения компонент этой непрерывной двумерной случайной величины?

Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения: . (8.2)

Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δ х и Δ у к площади этого прямоугольника при

Свойства двумерной плотности вероятности.

1) f (x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2) (cледует из определения двумерной плотности вероятно-сти).

3) (поскольку это вероятность того, что точка попадет на плос-кость О ху, то есть достоверного события).