Погрешности косвенных измерений

Большинство физических величин определяется косвенными путями. Сначала производится непосредственное, т.е. прямое измерение одной или нескольких физических величин, количественно связанных с определяемой величиной. Затем, с помощью соответствующих формул, вычисляется значение определяемой величины 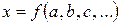. Очевидно, при этом ошибка вычисления зависит как от величины погрешностей прямых измерений исходных величин 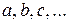, так и от функциональной связи между ними.

Пусть величины 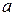и 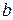получены прямым измерением со средними абсолютными погрешностям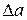и и :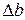

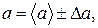
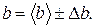
1. Измеряемая величина 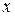равна сумме 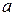и 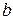, т.е. 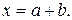Тогда 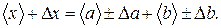Среднее значение величины 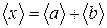и средняя абсолютная погрешность 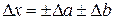. Так как неизвестно, в какую сторону допущены погрешност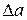и и 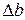, то рассматривают наименее выгодный случай, когда абсолютные погрешност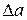и и 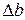одного знака

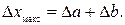
Наибольшая средняя абсолютная погрешность суммы измеряемых величин равна сумме средних абсолютных погрешностей слагаемых.

2. Измеряемая величина 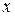равна разност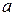и и 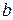, т.е. 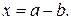Это соответствует случаю, когда погрешности уменьшаемого и вычитаемого имеют разные знаки. Следовательно, наибольшая погрешность разности измеряемых величин равна сумме погрешностей уменьшаемого и вычитаемого, т.е.

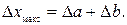
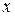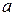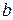3. Измеряемая величина равна произведению и , т.е.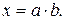

Наибольшая погрешность произведения двух сомножителей равна сумме произведений первого множителя на абсолютную погрешность второго и второго множителя на абсолютную погрешность первого, т.е.

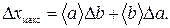
Следствие.

Абсолютная погрешность степени 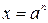равна

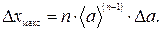
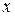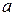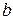4. Измеряемая величина определяется отношением и , т.е.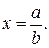

Наибольшая абсолютная погрешность дроби равна сумме произведений числителя на абсолютную погрешность знаменателя и знаменателя на абсолютную погрешность числителя, деленной на квадрат знаменателя, т.е.

Таким образом, средние абсолютные погрешности можно находить по правилам дифференцирования функций, заменив затем знак дифференциала 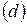знаком абсолютной ошибки 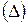. При этом необходимо учесть, что знаки у слагаемых в конечном выражении выбираются такими, чтобы средняя абсолютная погрешность получилась наибольшей.