Таблица расчета погрешностей

Функция x	Погрешности
	абсолютные	относительные

 

 

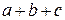
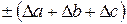
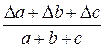
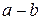
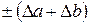
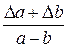
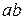
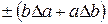
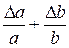
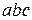
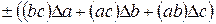
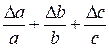
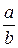
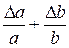
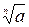
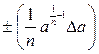
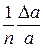
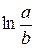
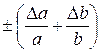
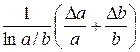
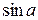
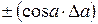
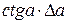
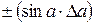
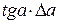
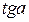
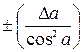
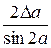
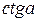
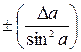
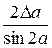
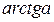
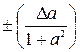
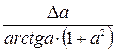
Относительная погрешность косвенного измерения равна

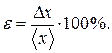
Часто формула для вычисления искомой величины представляет собой сложную зависимость от нескольких переменных. В таких случаях порядок вычисления абсолютной и относительной погрешностей целесообразно поменять местами, т.е. сначала вычислить относительную погрешность, а затем абсолютную.

Из математики известно, что 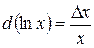. Заменяя в этом выражении  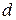на знак 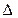, получим

.

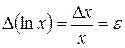Отсюда видно, что для нахождения относительной погрешности необходимо вначале прологарифмировать исходное выражение, а затем его продифференцировать и в конечном выражении заменить знак дифференциала 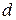 знаком .

 

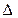Пример 1. Получим формулу для расчета относительной погрешности определения ускорения свободного падения  методом математического маятника. Прологарифмируем выражение 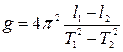, используемое в лабораторной работе, а затем продифференцируем.

 

;

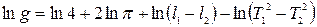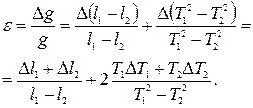
После вычисления 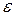 определяется абсолютная погрешность результата:

 

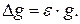
Пример 2. Вычислим ошибку в определении объема шара по измеренному радиусу. Пусть радиус шара:

 

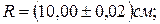
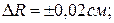
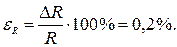
Объем шара подсчитывается по формуле:

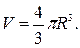
Тогда, абсолютная ошибка вычисления объема шара:

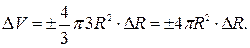
Подставим числовые значения:

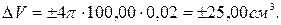
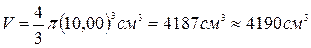 или

Прологарифмируем формулу объема:

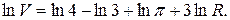
Тогда, относительная ошибка:

 Таким образом,

 

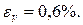
Пример 3. Рассчитать предельную ошибку вычисления объема прямоугольного параллелепипеда по данным измерений его ребер:

 

; ; .

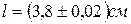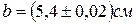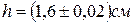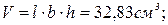
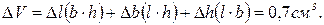
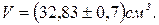
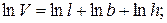
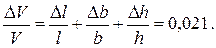
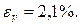
При измерениях электрических величин имеют место следующие основные погрешности.

Абсолютная погрешность 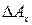  – алгебраическая разность между результатом измерения величины  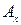и ее действительным значением :

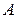Относительная погрешность отношение абсолютной погрешности измеряемой величины к ее действительному значению 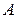, выраженному в процентах:

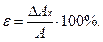
При тщательных измерениях с использованием наиболее точных приборов обычно 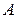и 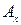мало отличаются друг от друга. Поэтому в выражении для относительной погрешности в качестве действительного значения  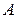берут величину 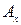, полученную из опыта. Погрешност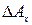и и 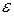 называют погрешностями измерения. Они зависят от погрешности отсчета и погрешности самих приборов.

Погрешность отсчета порождается самим наблюдателем. Для уменьшения этой погрешности проводят несколько отчетов: 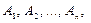и за результат измерения принимают среднее арифметическое:

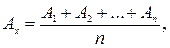
где 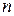  – число произведенных измерений.

Погрешность самих приборов называют относительной приведенной погрешностью. Она равна отношению абсолютной погрешности прибора 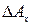к нормирующему значению 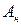, выраженному в процентах:

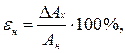
где 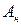– значение, соответствующее делению конца рабочей части шкалы для равномерных или степенных шкал с нулевой отметкой на краю или вне шкалы. Для таких же шкал с нулевой отметкой внутри рабочей части шкалы нормирующее значение принимается равным величине арифметической сумме конечных значений рабочей части шкалы (без учета знаков).