Решение (вариант «а»)

1. Выбираем исходную систему координат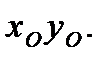

2. Разбиваем фигуру на простые составляющие (рис.2, а).

3. Определяем площади и координаты центров тяжести составных частей фигуры.

                                   

                                                     

                                     

 

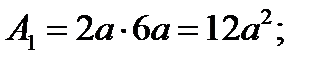
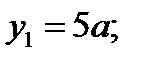
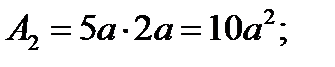
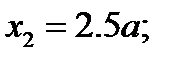
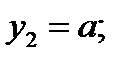
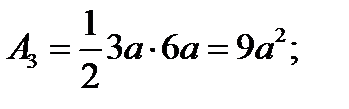
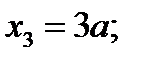
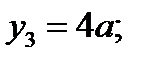
Рис.2.

 

4. Определяем общую площадь фигуры и вес плиты (равнодействующую системы параллельных сил).

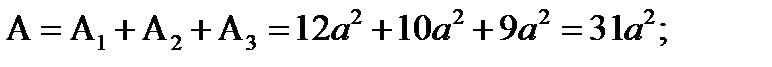
5. Определяем точку приложения равнодействующей (координаты центра тяжести) и показываем ее на рисунке.

      

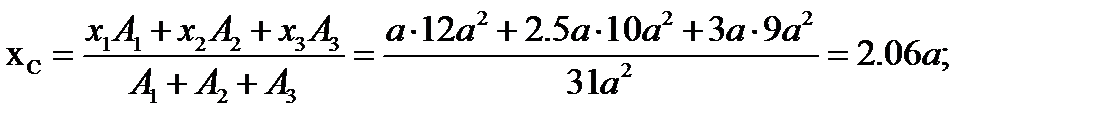
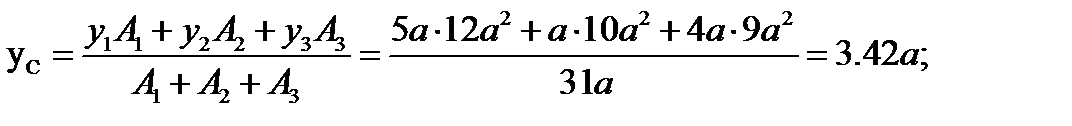
Решение задачи может стать более простым, если

· использовать «метод отрицательных площадей» и

· поместить начало исходной системы координат в центр тяжести одной из составляющих фигур.

 

Решение (вариант «б»)

1. Выбираем исходную систему координат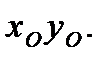

2. Разбиваем фигуру на простые составляющие (рис. 2, б).

3. Определяем площади и координаты центров тяжести составных частей фигуры.

                                   

                                                     

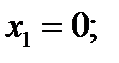
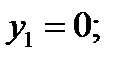
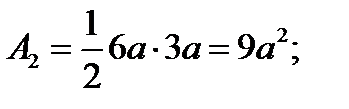
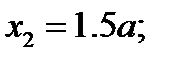
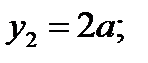
4. Определяем общую площадь фигуры.

5. Определяем координаты центра тяжести всей фигуры и показываем его на рисунке.

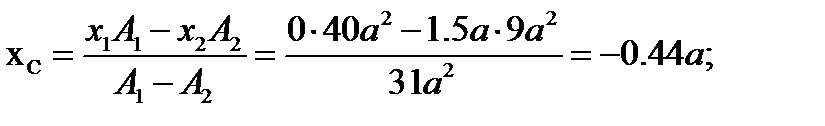
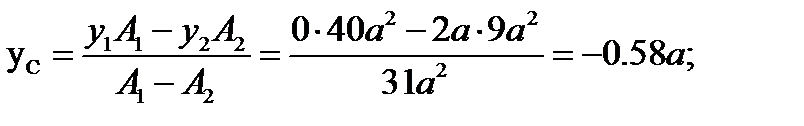
Задача 2

Определить положение центра тяжести плоской фигуры, показанной на рис. 3

Решение

1. Разбиваем фигуру на простые составляющие (рис. 4).

2. Выбираем исходную систему координат 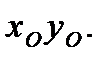 Для упрощения решения задачи начало исходной системы координат О совместим с центром тяжести первой фигуры и ось  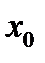направим по оси симметрии. В этом случае неизвестным остается положение центра тяжести фигуры на этой оси, то есть координата .

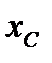Рис. 3.

 

Рис. 4.

3. Определяем площади и координаты центров тяжести частей фигуры.

                                      

                                                      

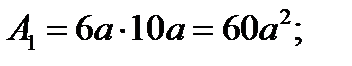
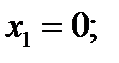
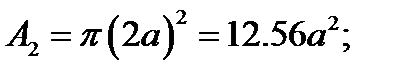
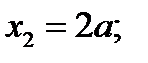
4. Определяем общую площадь фигуры.

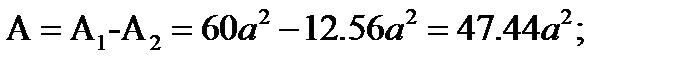
6. Определяем координаты центра тяжести всей фигуры и показываем его на рисунке.

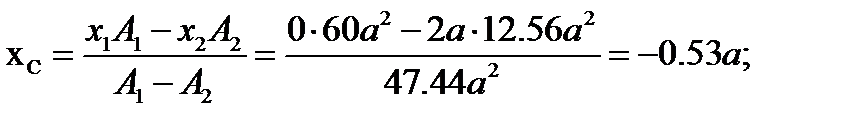
Задача 3

       Дано: вес 1м² плиты равен .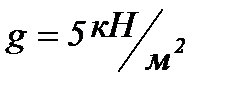

       Определить реакции связей на опорах 1,2 и 3.

       Решение

1. Выбираем исходную систему координат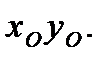

2. Разбиваем фигуру на простые составляющие.

Рис. 5.

 

Рис. 6.

3. Определяем площади и координаты центров тяжести составных частей фигуры.

                                     

                                                       

                                    

                                    

                               

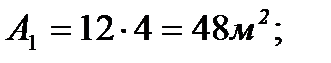
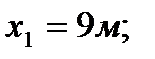
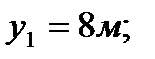
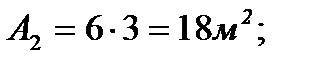
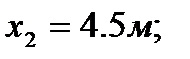
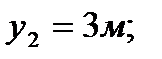
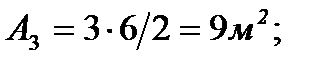
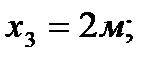
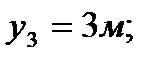
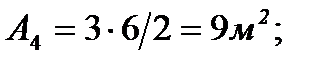
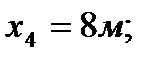
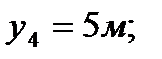
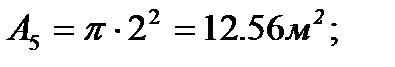
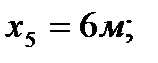
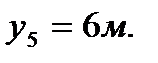
4. Определяем общую площадь фигуры и вес плиты (равнодействующую системы параллельных сил).

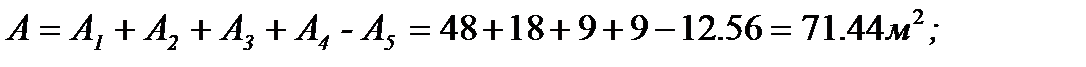
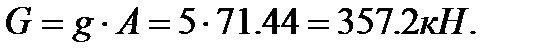
5. Определяем точку приложения равнодействующей (координаты центра тяжести) и показываем ее на рисунке.

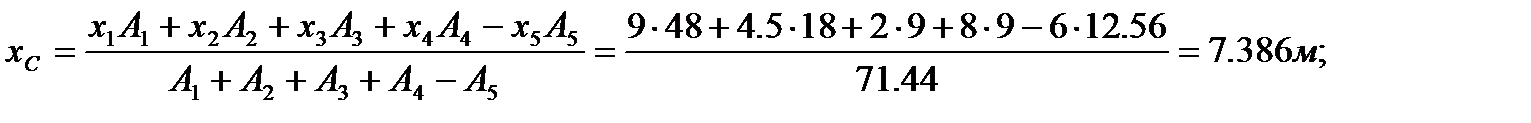
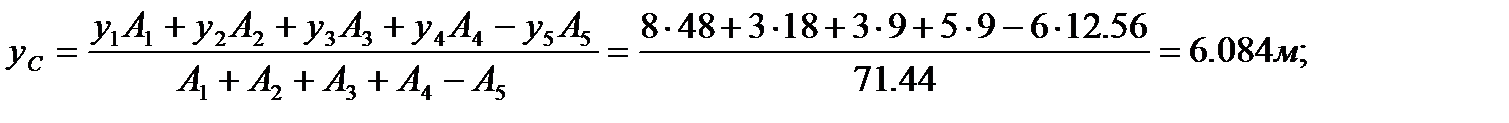
Рис. 5.

Рис. 6.

       Составляем уравнения равновесия, используя систему координатных осей uv, проходящих через точки опирания плиты.

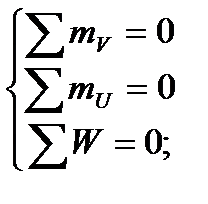
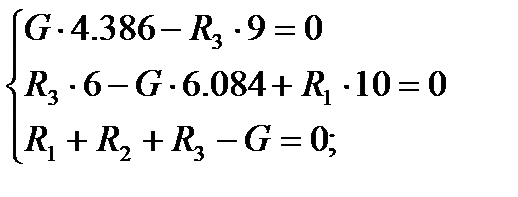
6. Решая систему уравнений, определяем реакции опор.

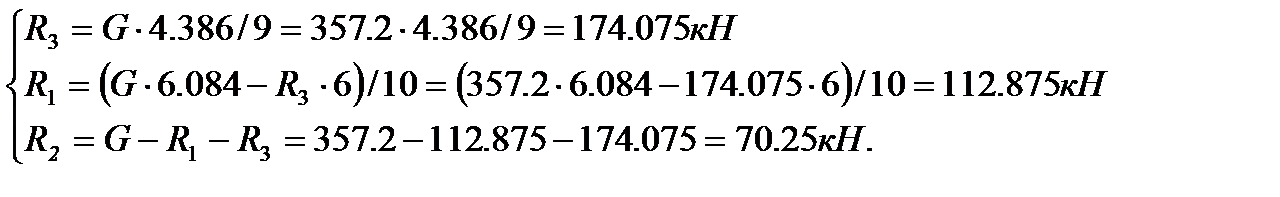
Ответ: реакции стоек равны , , .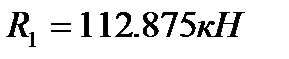

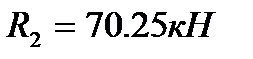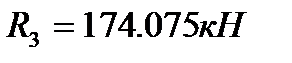Тема 9

 

 

Тема 10

 

 

Тема 11

 

 

Тема 12

 

 

Тема 13

 

 

Тема 14

 

 

Тема 15

 

 

Тема 16

 

 

Тема 17