Цели урока: 1. Показать соответствие каждому действительному числу единственной точке на окружности.
Дать определение функциям синус, косинус, тангенс и котангенс.
Мы рассматриваем числовую окружность с центром в начале координат, 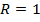 и началом отсчета в точке
и началом отсчета в точке 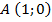 , как показано на рисунке 1.
, как показано на рисунке 1.
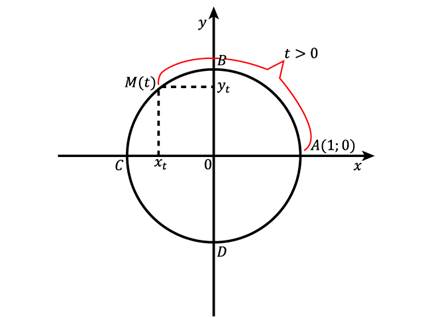
Рис. 1. Числовая окружность
Каждому действительному числу 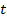 соответствует единственная точка
соответствует единственная точка 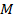 на этой окружности (рис. 1).
на этой окружности (рис. 1).
Каждая точка 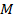 имеет единственную пару декартовых координат: абсциссу
имеет единственную пару декартовых координат: абсциссу 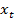 и ординату
и ординату 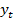 (рис. 1). Имеем действительное число
(рис. 1). Имеем действительное число 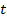 , по нему находим единственную точку на окружности
, по нему находим единственную точку на окружности 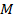 , а эта единственная точка на окружности имеет единственную пару декартовых координат
, а эта единственная точка на окружности имеет единственную пару декартовых координат 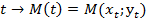 .
.
Таким образом, каждому действительному числу 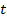 сопоставляется два числа
сопоставляется два числа 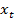 и
и 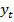 . Имеем функции
. Имеем функции 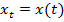 и
и 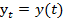 .
.
Далее этим функциям будут даны специальные названия 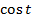 и
и 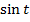 . С каждой функцией связано две основные задачи.
. С каждой функцией связано две основные задачи.
Прямая задача
По заданному 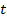 найти значение функции
найти значение функции 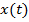 и
и 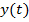 .
.
Обратная задача
По заданному значению зависимой переменной 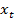 или
или 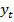 найти все соответствующие значения аргумента
найти все соответствующие значения аргумента 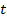 . То есть найти множество всех значений аргумента, при которых зависимая переменная достигает заданного значения. Обратная задача имеет бесчисленное множество решений.
. То есть найти множество всех значений аргумента, при которых зависимая переменная достигает заданного значения. Обратная задача имеет бесчисленное множество решений.
Решение вида t+2πn;
Числам 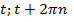 соответствует одна и та же единственная точка
соответствует одна и та же единственная точка 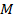 на окружности, то есть
на окружности, то есть 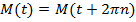 .
.
Почему же точкам 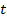 и
и 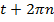 соответствует одна и та же точка
соответствует одна и та же точка 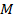 на окружности?
на окружности?
Потому, что 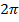 – длина единичной окружности. Ведь длина окружности
– длина единичной окружности. Ведь длина окружности 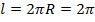 , так как
, так как 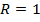 . Сделав полный оборот, из точки
. Сделав полный оборот, из точки 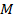 мы снова попадаем в точку
мы снова попадаем в точку 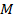 . Число
. Число 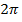 далее будет называться наименьшим положительным периодом функции
далее будет называться наименьшим положительным периодом функции 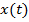 и
и 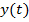 .
.
Рассмотрим еще один пример. Пусть точка 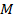 соответствует на циферблате числу 1, и часовая стрелка указала на эту точку числа
соответствует на циферблате числу 1, и часовая стрелка указала на эту точку числа 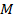 , то есть на 1, один час. Но если мы находимся в комнате без окон, то мы не сможем определить, что это, час дня или час ночи. Этот пример иллюстрирует неоднозначность решения обратной задачи.
, то есть на 1, один час. Но если мы находимся в комнате без окон, то мы не сможем определить, что это, час дня или час ночи. Этот пример иллюстрирует неоднозначность решения обратной задачи.
Задача 1.
Дано действительное 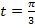 .
.
Найти: место расположения точки 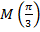 и ее декартовы координаты
и ее декартовы координаты 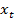 и
и 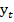 .
.
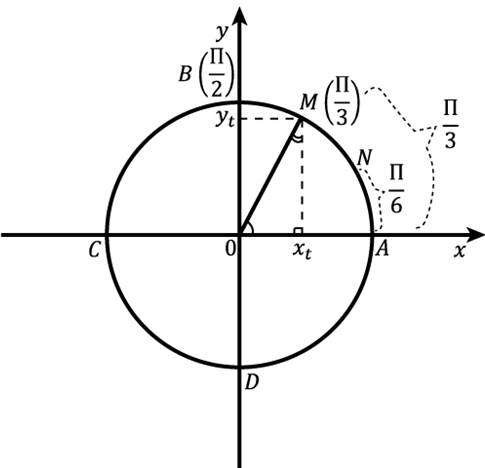
Рис. 2. Первый способ нахождения точки 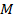
Решение
Точку 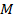 можно найти несколькими способами.
можно найти несколькими способами.
Первый способ нахождения точки M
Дугу 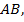 равную
равную 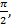 разделим на 3 равные части (рис. 2). Каждая часть – это
разделим на 3 равные части (рис. 2). Каждая часть – это  . Значит, точка
. Значит, точка 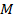 имеет координату
имеет координату 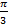 , так как
, так как 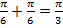 .
.
 2020-05-21
2020-05-21 149
149







