2020-05-25
363
Фрикционное безнапорное движение жидкости, когдаодна из стенок, образующих зазор, перемещается параллельно другой, например, при движении пластинки положенной на жидкость и неподвижном дне сосуда, при отсутствии давления в зазоре. Подвижная стенка увлекает за собой жидкость.
Рассматриваем равновесие в потоке элемента dx*dy*b, как показано на рис.6.
Давления, приложенные к левой и правой граням элемента одинаковы (напора – нет). Hа элемент действуют силы трения, вызываемые касательными напряжениями на нижней грани – τ и на верхней грани τ+δ τ. Из-за неодинаковой скорости по сечению элемент жидкости притормаживается снизу
Рис. 6.Фрикционное безнапорное движение
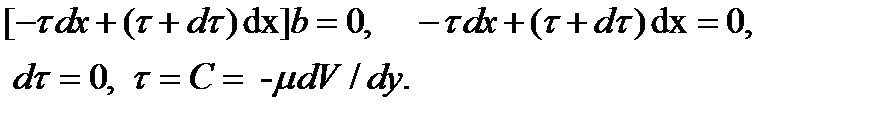
После ещё одного интегрирования
Постоянные С и С1 найдём при y = а/2, V = u0/2 и при y = a, V = u0. Отсюда
где u0– скорость стенки, а – ширина зазора.
После подстановки С и С1 в последнее уравнение получим закон распределения скоростей при безнапорном течении
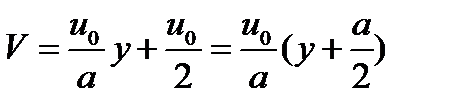
Расход жидкости q определяется по средней скорости y=0,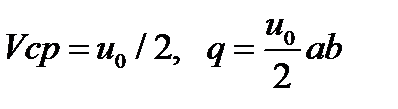 
.
Если перемещение жидкости происходит при перепаде давления в жидкости, заполняющей зазор, то закон распределения скоростей найдём, как сумму или разность для напорного и фрикционного движения жидкости.
Скорость напорного движения
Скорость фрикционного движения 
При совпадении силы давления жидкости и направления движения стенки сумма скоростей 
При несовпадении 
Рис. 8. Напорное и фрикционное движение с одной движущейся стенкой. а) движется верхняя стенка, б) движется нижняя стенка
Распределение скоростей в зазоре показано на рис. 8 в двух вариантах:
а) направление движения стенки совпадает с направление течения жидкости под действием перепада давлений;
б) направление движения стенки противоположно течению жидкости.
Расход жидкости через зазор единичной ширины в этих случаях определится как сумма расходов, выражаемых предыдущими формулами, для b=1
где 
- скорость напорного, u0- безнапорного движения.
Первое слагаемое формулы называется расходом напорного течения, а второе — фрикционным расходом.
