Теорема 10.2.1. Если язык L является контекстно-свободным, то существует МП-автомат, распознающий этот язык.
Доказательство. Пусть язык L порождается контекстно-свободной грамматикой 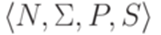 , в которой каждое правило имеет вид
, в которой каждое правило имеет вид  , где
, где  ,
, 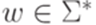 и
и  (в силу теоремы 8.8.3 такая грамматика существует). Положим
(в силу теоремы 8.8.3 такая грамматика существует). Положим  ,
,  ,
,  ,
,  и
и
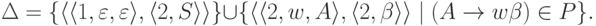
Можно доказать, что  тогда и только тогда, когда существует левосторонний вывод
тогда и только тогда, когда существует левосторонний вывод  (здесь
(здесь 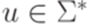 и
и 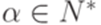 ).
).
Пример 10.2.2. Пусть 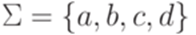 . Контекстно-свободная грамматика
. Контекстно-свободная грамматика
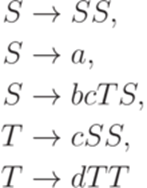
и МП-автомат 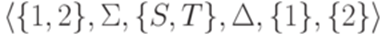 , где
, где

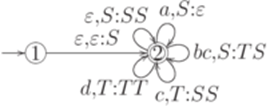
задают один и тот же язык.
Лемма 10.2.3. Каждый МП-автомат эквивалентен некоторому МП-автомату 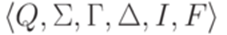 , где |I| = 1, |F| = 1 и каждый переход
, где |I| = 1, |F| = 1 и каждый переход  удовлетворяет требованиям
удовлетворяет требованиям  и
и 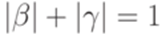 .
.
Пример 10.2.4. Рассмотрим МП-автомат  , где
, где 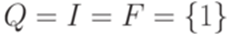 ,
, 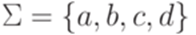 ,
, 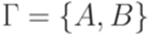 ,
,
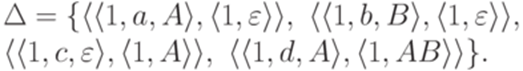

Он эквивалентен МП-автомату 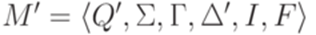 , где
, где  и
и

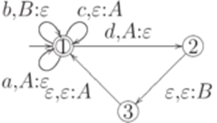
Пример 10.2.5. Рассмотрим МП-автомат  , где
, где  ,
, 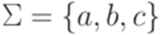 ,
,  ,
,
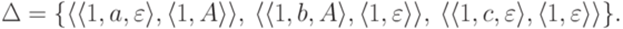
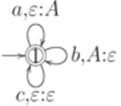
Он эквивалентен МП-автомату  , где
, где 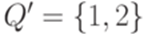 ,
, 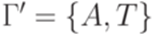 и
и

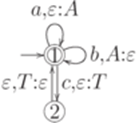
Пример 10.2.6. Рассмотрим МП-автомат 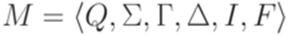 , где
, где  ,
,  ,
, 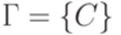 ,
,
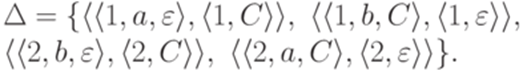
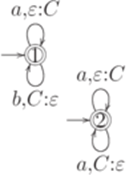
Он эквивалентен МП-автомату 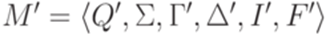 , где
, где 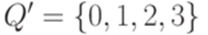 ,
, 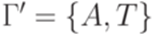 ,
, 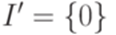 ,
,  ,
,
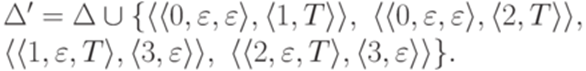

Теорема 10.2.7. Если язык L распознается некоторым МП-автоматом, то L является контекстно-свободным.
Доказательство. Пусть язык L распознается МП-автоматом  . Без ограничения общности можно считать, что
. Без ограничения общности можно считать, что 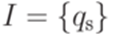 ,
,  и каждый переход
и каждый переход 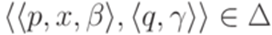 удовлетворяет требованию
удовлетворяет требованию 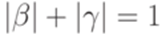 . Построим искомую контекстно-свободную грамматику
. Построим искомую контекстно-свободную грамматику 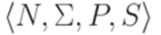 , положив
, положив  ,
,  и
и
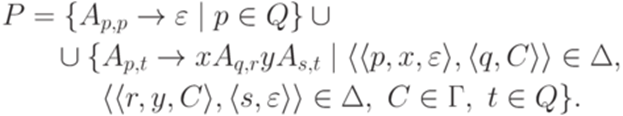
Можно доказать, что  тогда и только тогда, когда
тогда и только тогда, когда 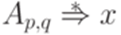 (здесь
(здесь 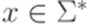 ).
).
Пример 10.2.8. МП-автомат  , где
, где  ,
, 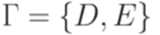 ,
,
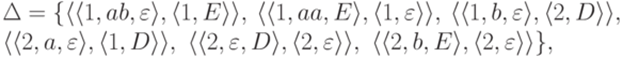
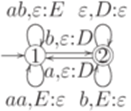
и контекстно-свободная грамматика
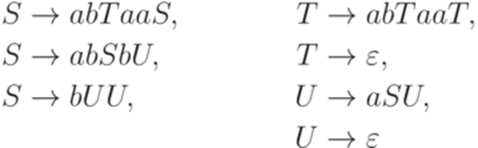
задают один и тот же язык. Здесь S, T и U соответствуют символам A1,2, A1,1 и A2,2 из доказательства теоремы 10.2.7.
Упражнение 10.2.9. Найти МП-автомат, распознающий язык, порождаемый грамматикой

Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 
Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 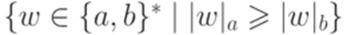
Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 
10.3*. Автоматы с магазинной памятью с однобуквенными переходами
Теорема 10.3.1. Каждый МП-автомат эквивалентен некоторому МП-автомату 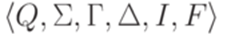 , где |Q| = 2 и каждый переход
, где |Q| = 2 и каждый переход 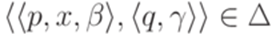 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.
Доказательство. Пусть исходным МП-автоматом распознается контекстно-свободный язык 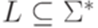 . Согласно теореме 8.4.6 язык
. Согласно теореме 8.4.6 язык 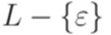 порождается некоторой контекстно-свободной грамматикой
порождается некоторой контекстно-свободной грамматикой 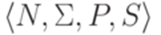 , в которой каждое правило имеет вид
, в которой каждое правило имеет вид 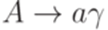 , где
, где 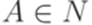 ,
, 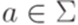 ,
,  и
и  . Аналогично тому, как было сделано при доказательстве теоремы 10.2.1, положим
. Аналогично тому, как было сделано при доказательстве теоремы 10.2.1, положим  , Q = {1,2}, I = {1},
, Q = {1,2}, I = {1},

Теорема 10.3.2. Каждый МП-автомат эквивалентен некоторому МП-автомату 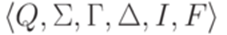 , в котором каждый переход
, в котором каждый переход 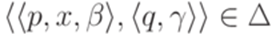 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.
Доказательство. Пусть исходным МП-автоматом распознается контекстно-вободный язык  . Согласно теореме 8.4.6 язык
. Согласно теореме 8.4.6 язык 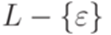 порождается некоторой контекстно-вободной грамматикой
порождается некоторой контекстно-вободной грамматикой 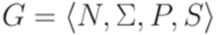 , в которой каждое правило имеет один из следующих трех видов:
, в которой каждое правило имеет один из следующих трех видов: 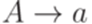 ,
, 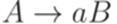 ,
, 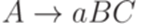 , где
, где 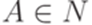 ,
, 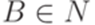 ,
, 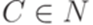 ,
, 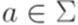 . Легко добиться того, чтобы в правилах грамматики G вспомогательные символы в правой части (то есть символы B и C) были отличны от начального символа S.
. Легко добиться того, чтобы в правилах грамматики G вспомогательные символы в правой части (то есть символы B и C) были отличны от начального символа S.
Положим 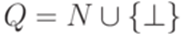 , где
, где 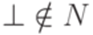 . Далее, положим
. Далее, положим 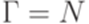 ,
,
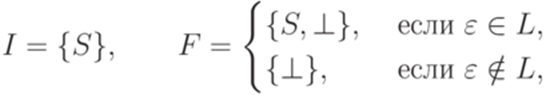
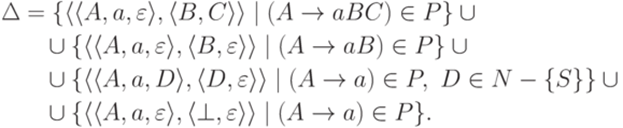
Упражнение 10.3.3. Найти для языка, порождаемого грамматикой
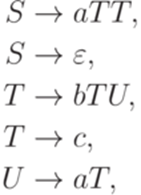
МП-автомат, в котором каждый переход 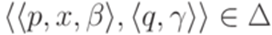 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.
Упражнение 10.3.4. Найти для языка, порождаемого грамматикой

МП-автомат, в котором каждый переход 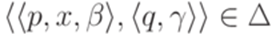 удовлетворяет требованиям
удовлетворяет требованиям  ,
,  и
и  .
.
В этой лекции излагаются те свойства контекстно-свободных языков, которые удобно доказывать с привлечением автоматов с магазинной памятью. В первых двух разделах приводятся некоторые свойства замкнутости класса контекстно-свободных языков (замкнутость относительно деления, взятия гомоморфного образа и полного гомоморфного прообраза). В конце лекции формулируются два критерия контекстной свободности, интересных в основном с теоретической точки зрения.
11.1*. Деление контекстно-свободных языков
Теорема 11.1.1. Пусть L1 - контекстно-свободный язык над алфавитом 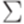 и L2 - автоматный язык над алфавитом
и L2 - автоматный язык над алфавитом 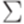 . Тогда язык
. Тогда язык 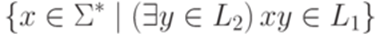 является контекстно-свободным.
является контекстно-свободным.
Доказательство. Пусть 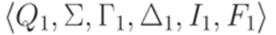 - МП-автомат, распознающий язык L1. Без ограничения общности можно считать, что для каждого перехода
- МП-автомат, распознающий язык L1. Без ограничения общности можно считать, что для каждого перехода 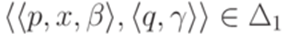 выполняется неравенство
выполняется неравенство  .
.
Пусть 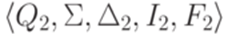 - конечный автомат, распознающий язык L2. Без ограничения общности можно считать, что
- конечный автомат, распознающий язык L2. Без ограничения общности можно считать, что

и для каждого перехода  выполняется равенство |x| = 1.
выполняется равенство |x| = 1.
Тогда язык 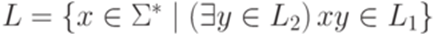 распознается МП-автоматом
распознается МП-автоматом 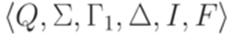 , где
, где 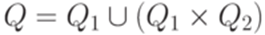 , I = I1,
, I = I1,  и
и
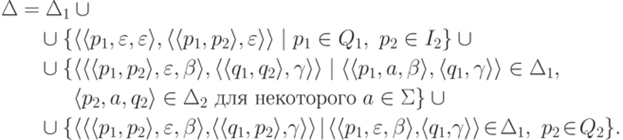
Пример 11.1.2. Пусть  , язык L1 распознается МП-автоматом
, язык L1 распознается МП-автоматом

и язык L2 распознается конечным автоматом

Следуя доказательству теоремы 11.1.1, получаем, что язык
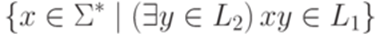
распознается МП-автоматом, изображенным ниже.
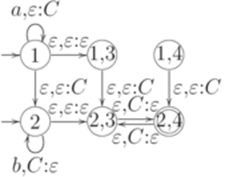
Пример 11.1.3. Пусть  ,
,  и
и 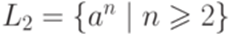 . Тогда
. Тогда
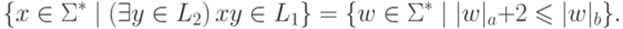
Пример 11.1.4. Пусть  ,
,  и
и 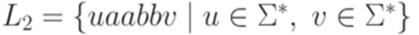 . Тогда
. Тогда
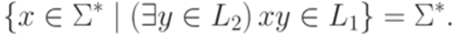
Замечание 11.1.5. Пусть 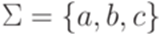 и
и 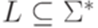 . Язык
. Язык  является контекстно-свободным тогда и только тогда, когда язык L является контекстно-свободным.
является контекстно-свободным тогда и только тогда, когда язык L является контекстно-свободным.
Упражнение 11.1.6. Существует ли такой контекстно-свободный язык 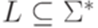 , что язык Subw не является контекстно-свободным?
, что язык Subw не является контекстно-свободным?
Упражнение 11.1.7. Существует ли такой контекстно-свободный язык L над алфавитом {a,b}, что язык 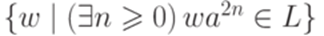 не является контекстно-свободным?
не является контекстно-свободным?
Упражнение 11.1.8. Существует ли такой контекстно-свободный язык L над алфавитом {a,b}, что язык

 2020-05-25
2020-05-25 209
209








