Теорема 11.2.1. Для любого гомоморфизма  и контекстно-свободного языка
и контекстно-свободного языка 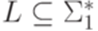 язык h(L) является контекстно-свободным.
язык h(L) является контекстно-свободным.
Доказательство. Приведем здесь доказательство, использующее МП-автоматы, хотя эту теорему легко доказать и с помощью контекстно-свободных грамматик. Пусть язык L распознается МП-автоматом 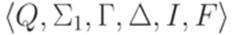 . Тогда язык h(L) распознается МП-автоматом
. Тогда язык h(L) распознается МП-автоматом 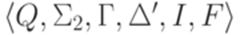 , где
, где
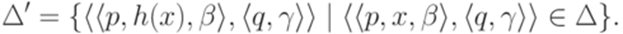
Пример 11.2.2. Пусть 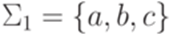 и
и 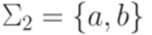 . Рассмотрим контекстно-свободный язык L, порождаемый грамматикой
. Рассмотрим контекстно-свободный язык L, порождаемый грамматикой
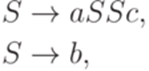
и гомоморфизм  , заданный равенствами h(a) = a, h(b) = bba и h(c) = a. Тогда язык h(L)порождается контекстно-свободной грамматикой
, заданный равенствами h(a) = a, h(b) = bba и h(c) = a. Тогда язык h(L)порождается контекстно-свободной грамматикой
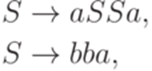
Упражнение 11.2.3. Пусть гомоморфизм  задан соотношениями h(a) = b,
задан соотношениями h(a) = b, 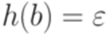 , h(c) = a. Рассмотрим язык L, порождаемый грамматикой
, h(c) = a. Рассмотрим язык L, порождаемый грамматикой
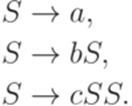
Найти контекстно-свободную грамматику для языка h(L).
Теорема 11.2.4. Для любого гомоморфизма  и контекстно-свободного языка
и контекстно-свободного языка 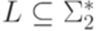 язык h-1(L) является контекстно-свободным.
язык h-1(L) является контекстно-свободным.
Доказательство. Введем обозначение
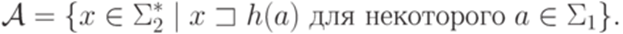
Пусть язык L распознается МП-автоматом 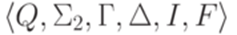 . Без ограничения общности можно считать, что для каждого перехода
. Без ограничения общности можно считать, что для каждого перехода 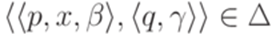 выполняется неравенство
выполняется неравенство  . Можно проверить, что в этом случае язык h-1(L) распознается МП-автоматом
. Можно проверить, что в этом случае язык h-1(L) распознается МП-автоматом 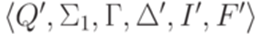 , где
, где
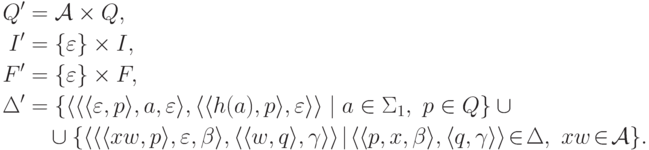
Пример 11.2.5. Пусть 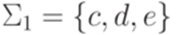 и
и 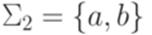 . Рассмотрим гомоморфизм
. Рассмотрим гомоморфизм  , заданный равенствами h(c) = aa, h(d) = b и h(e) = bba. Пусть контекстно-свободный язык L распознается МП-автоматом
, заданный равенствами h(c) = aa, h(d) = b и h(e) = bba. Пусть контекстно-свободный язык L распознается МП-автоматом 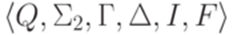 , где Q = {p},
, где Q = {p},  , I = {p}, F = {p},
, I = {p}, F = {p},
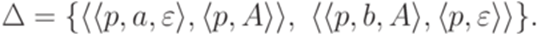

Тогда язык h-1(L) распознается МП-автоматом 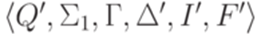 , где
, где 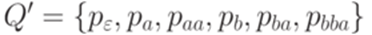 ,
, 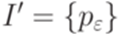 ,
, 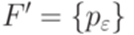 и
и
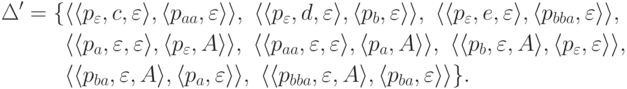
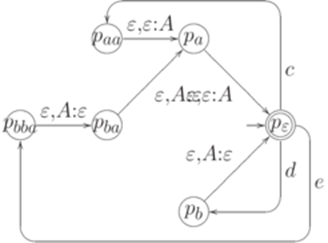
Язык h-1(L) также порождается контекстно-свободной грамматикой 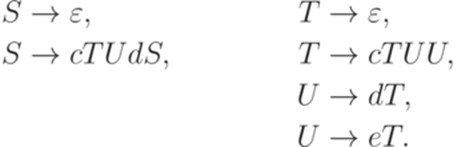
Упражнение 11.2.6. Пусть гомоморфизм  задан соотношениями h(a) = ab, h(b) = aaba, h(c) = b. Рассмотрим язык L, порождаемый грамматикой
задан соотношениями h(a) = ab, h(b) = aaba, h(c) = b. Рассмотрим язык L, порождаемый грамматикой
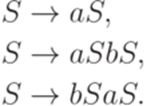
Описать язык h-1(L).
Упражнение 11.2.7. 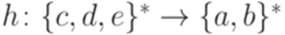 задан соотношениями h(c) = a, h(d) = ba, h(e) = bb. Рассмотрим язык L, порождаемый грамматикой
задан соотношениями h(c) = a, h(d) = ba, h(e) = bb. Рассмотрим язык L, порождаемый грамматикой
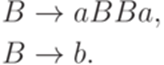
Найти контекстно-свободную грамматику для языка h-1(L).
Упражнение 11.2.8. Пусть гомоморфизм 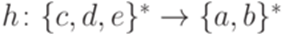 задан соотношениями
задан соотношениями  ,
, 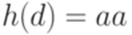 ,
, 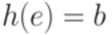 . Рассмотрим язык
. Рассмотрим язык 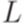 , порождаемый грамматикой
, порождаемый грамматикой
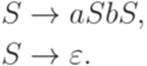
Найти контекстно-свободную грамматику для языка h-1(L).
Упражнение 11.2.9. Обозначим через L язык, порождаемый грамматикой
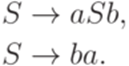
Рассмотрим гомоморфизм 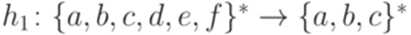 , заданный соотношениями
, заданный соотношениями
и гомоморфизм 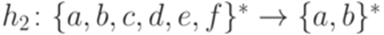 , заданный соотношениями
, заданный соотношениями
Найти контекстно-свободную грамматику, порождающую язык
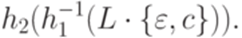
 2020-05-25
2020-05-25 160
160








