Представления контекстно-свободных языков посредством гомоморфизмов

Теорема 11.3.1. Рассмотрим алфавит и язык , порождаемый контекстно-свободной грамматикой G₀:

Произвольный язык 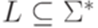является контекстно-свободным тогда и только тогда, когда существует такой гомоморфизм , что L = h^-1(L₀) или .

Доказательство. Достаточность следует из теоремы 11.2.4. Приведем теперь идею доказательства необходимости (полное доказательство можно найти в [Сал, с. 103-109]).

Пусть дан произвольный контекстно-свободный язык L. Согласно теореме 8.4.6 язык порождается некоторой контекстно-свободной грамматикой , в которой каждое правило имеет один из следующих трех видов: , , , где .

Определим вспомогательную функцию , ставящую в соответствие каждому символу из 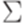конечный язык над алфавитом следующим образом:

Искомый гомоморфизм h определяется следующим образом: если

положим

Пример 11.3.2. Пусть . Рассмотрим язык L, порождаемый грамматикой

Тогда L = h^-1(L₀), где гомоморфизм h задан равенствами

h(d) = cb₁b₂b₁a₁a₂a₂a₁a₁a₂a₁c,h(f) = cb₁b₂b₁cb₁b₂b₂b₁a₁a₂a₂a₂a₁cb₁b₂b₂b₁a₁a₂a₂a₂a₁a₁a₂a₂a₁c,h(g) = cb₁b₂b₂b₂b₁c.

Рассмотрим, например, слово . Проверим, что слово h(dffg) выводится в грамматике G₀ из теоремы 11.3.1. Очевидно, что 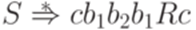. С помощью последних пяти правил грамматики G₀ можно вывести, что

Осталось найти такие шесть выводимых из C слов , что

Подходят слова

w₁ = c,w₂ = c,w₃ = cb₁b₂b₂b₁a₁a₂a₂a₂a₁cb₁b₂b₂b₁a₁a₂a₂a₂a₁a₁a₂a₂a₁c,w₄ = cb₁b₂b₁c,w₅ = cb₁b₂b₂b₁a₁a₂a₂a₂a₁a₁a₂a₂a₁c,w₆ = c.

Теорема 11.3.3 (Теорема Хомского-Шютценберже). Язык является контекстно-свободным тогда и только тогда, когда существуют такие натуральное число n, автоматный язык L₁ над алфавитом и гомоморфизм , что , где - язык Дика над 2n буквами.

Доказательство можно найти в [Лал, с. 331-333].

Упражнение 11.3.4. Рассмотрим язык L₁, порождаемый грамматикой

и язык L₂, порождаемый грамматикой

Найти такой гомоморфизм , что

К сожалению, теорема о детерминизации не переносится с конечных автоматов на автоматы с магазинной памятью. Возникает важный для практических приложений класс языков, распознаваемых детерминированными автоматами с магазинной памятью (то есть такими автоматами с магазинной памятью, которые ни в какой конфигурации не могут выбирать между несколькими очередными тактами). Точные определения этого класса автоматов и соответствующего класса языков даны в разделе 12.1. Чтобы получить полезный и естественный с точки зрения практики класс, нужно добавить в конец каждого слова специальный символ, называемый маркером конца слова. Языки из выделенного таким образом класса называются детерминированными контекстно-свободными языками. Во втором разделе лекции формулируется ряд свойств этого класса языков. Важность детерминированных контекстно-свободных языков для теоретической информатики обусловлена тем, что для каждого такого языка можно указать быстрый алгоритм, распознающий принадлежность слова этому языку.