Определение 10.1.1. Автомат с магазинной памятью (МП-автомат, магазинный автомат, стековый автомат, pushdown automaton) - это шестерка  , где
, где  ,
, 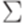 ,
, 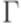 и
и  - конечные множества,
- конечные множества,  ,
,  и
и
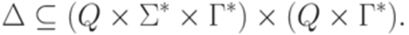
Здесь Q - множество состояний, 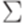 - входной алфавит,
- входной алфавит, 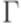 - алфавит магазинной памяти (stack alphabet),
- алфавит магазинной памяти (stack alphabet),  - множество переходов (transition relation), элементы I называются начальными состояниями, элементы F - заключительными или допускающими состояниями.
- множество переходов (transition relation), элементы I называются начальными состояниями, элементы F - заключительными или допускающими состояниями.
Пример 10.1.2. Пусть Q = {1,2},  ,
,  ,
,

 ,
,  . Тогда
. Тогда  - МП-автомат.
- МП-автомат.
Замечание 10.1.3. МП-автоматы можно изображать в виде диаграмм состояний. На диаграмме каждое состояние обозначается кружком, а переход - стрелкой. Каждое начальное состояние распознается по ведущей в него короткой стрелке. Каждое допускающее состояние отмечается на диаграмме двойным кружком. Стрелка с пометкой  , ведущая из p в q, показывает, что
, ведущая из p в q, показывает, что  является переходом данного МП-автомата.
является переходом данного МП-автомата.
Пример 10.1.4. Ниже приведена диаграмма МП-автомата из примера 10.1.2.

Определение 10.1.5. Конфигурацией МП-автомата называется любая тройка  , где
, где  ,
,  ,
,  .
.
Определение 10.1.6. Определим на множестве всех конфигураций МП-автомата  бинарное отношение
бинарное отношение  (такт работы) следующим образом. Если
(такт работы) следующим образом. Если  ,
,  и
и 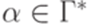 , то
, то  .
.
Замечание 10.1.7 Обычно из контекста ясно, о каком МП-автомате идет речь. Тогда вместо  будем писать
будем писать  .
.
Пример 10.1.8. Для МП-автомата из примера 10.1.2 выполняется 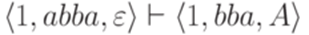 и
и  .
.
Определение 10.1.9. Бинарное отношение  определяется как рефлексивное, транзитивное замыкание отношения
определяется как рефлексивное, транзитивное замыкание отношения  .
.
Пример 10.1.10. Для МП-автомата из примера 10.1.2 выполняется  и
и 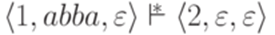 .
.
Лемма 10.1.11. Если  и
и  , то
, то  .
.
Доказательство. Лемму легко доказать индукцией по количеству тактов в вычислительном процессе, ведущем из конфигурации  в конфигурацию
в конфигурацию  .
.
Определение 10.1.12. Слово  допускается МП-автоматом
допускается МП-автоматом  , если найдутся такие состояния
, если найдутся такие состояния  и
и  , что
, что  .
.
Определение 10.1.13. Язык, распознаваемый МП-автоматом, - множество всех слов, допускаемых этим МП-автоматом. Язык, распознаваемый МП-автоматом M, обозначается L(M).
Замечание 10.1.14. Обычно в учебниках используется более узкое определение МП-автомата, но это не меняет класса языков, распознаваемых МП-автоматами.
Пример 10.1.15. Пусть 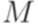 - МП-автомат из примера 10.1.2. Тогда
- МП-автомат из примера 10.1.2. Тогда  .
.
Пример 10.1.16. Пусть 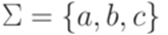 . Рассмотрим МП-автомат
. Рассмотрим МП-автомат  , где
, где  ,
,  , I = {1}, F = {4,5} и
, I = {1}, F = {4,5} и


Тогда  .
.
Определение 10.1.17. Два МП-автомата эквивалентны, если они распознают один и тот же язык.
Замечание 10.1.18. В данном пособии не рассматриваются преобразователи с магазинной памятью (pushdown transducer) обобщение автоматов с магазинной памятью посредством добавления "выходного" потока (см. [7, 3.5] или [2, 3.1.4]).
Замечание 10.1.19. Некоторые авторы изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом  , если найдутся такие состояния
, если найдутся такие состояния  и
и  и последовательность
и последовательность 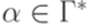 , что
, что  . Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
. Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
Замечание 10.1.20. Некоторые авторы добавляют в определение МП-автомата седьмую компоненту - Z0, называемую маркером магазинной памяти (start pushdown symbol), и изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом  , если найдутся такие состояния
, если найдутся такие состояния  и
и  , что
, что  . Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
. Такое определение не изменяет класса языков, распознаваемых МП-автоматами.
Замечание 10.1.21. Класс языков, распознаваемых МП-автоматами, не изменится также, если использовать следующую естественную комбинацию двух предыдущих определений: слово w допускается МП-автоматом  , если найдутся такие состояния
, если найдутся такие состояния  и
и  и последовательность
и последовательность  , что
, что  .
.
Замечание 10.1.22. Некоторые авторы добавляют в определение МП-автомата маркер магазинной памяти Z0, отбрасывают множество F и изменяют определение допускаемых слов следующим образом: слово w допускается МП-автоматом  , если найдутся такие состояния
, если найдутся такие состояния  и
и  , что
, что  . Это также не изменяет класса языков, распознаваемых МП-автоматами.
. Это также не изменяет класса языков, распознаваемых МП-автоматами.
Упражнение 10.1.23. Найти МП-автомат, распознающий язык 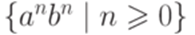
Упражнение 10.1.24. Найти МП-автомат, распознающий язык 
Упражнение 10.1.25. Найти МП-автомат, распознающий язык 
 2020-05-25
2020-05-25 117
117








