Проблема соответствий Поста

Определение 14.5.1. Постовской системой соответствия над алфавитом называется упорядоченная пара конечных последовательностей , где и для всех i.

Замечание 14.5.2. Систему иногда изображают в виде

Определение 14.5.3. Решением (match) постовской системы соответствия ((x₁,...,x_n),(y₁,...,y_n)) называется непустая последовательность индексов , удовлетворяющая условию

где для каждого j.

Пример 14.5.4. Пусть . Рассмотрим постовскую систему соответствия

Последовательность (2,1,3,2,2) является решением этой системы, так как

Упражнение 14.5.5. Пусть . Существует ли решение у постовской системы соответствия

Определение 14.5.6. Проблемой соответствий Поста (Post correspondence problem) называется проблема нахождения алгоритма, выясняющего для каждой постовской системы соответствия, существует ли решение этой системы.

Теорема 14.5.7. Пусть . Тогда не существует алгоритма, позволяющего по произвольной постовской системе соответствия над алфавитом 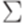узнать, имеет ли она решение. (Другими словами, проблема соответствий Поста неразрешима.)

Доказательство можно найти в [ХопМот, 9.4].

Упражнение 14.5.8. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.9. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.10. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.11. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.12. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.13. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.14. Существует ли решение у постовской системы соответствия ?

Упражнение 14.5.15. Существует ли постовская система соответствия, имеющая ровно одно решение?

В этой лекции рассматриваются наиболее известные разрешимые проблемы, связанные с грамматиками, автоматами и регулярными выражениями. Поскольку все приведенные выше доказательства эквивалентности разных способов конечного задания формального языка были конструктивными, не важно, какой из эквивалентных способов задания языка (например, посредством контекстно-свободной грамматики или автомата с магазинной памятью) используется в точной формулировке массовой задачи.

Первые два раздела этой лекции посвящены контекстным языкам. В разделах 15.3-15.6 сформулированы теоремы о разрешимости для некоторых алгоритмических проблем. Доказательства этих теорем опираются на конструктивность рассуждений, проведенных в лекциях "3" и "8". В разделе 15.7* приводится новый неожиданный результат, доказанный в 1997 году.

Проблема эквивалентности конечных автоматов (или, что то же самое, регулярных выражений) разрешима, но, к сожалению, она сложна, то есть нахождение ответа индивидуальной задачи требует (в некотором смысле) много времени. В разделе 15.9* указывается, что даже для регулярных выражений без итерации (которые, очевидно, соответствуют конечным автоматам без циклов) проблема неэквивалентности NP -полна (необходимые определения из теории сложности вычислений приведены в разделе 15.8*).