Определение 14.2.1. Говорят, что детерминированная машина Тьюринга
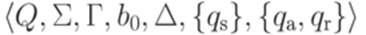
с выделенным состоянием qa разрешает (decides) язык 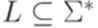 , если
, если
1) для каждого слова 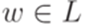 найдутся такие
найдутся такие 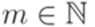 и
и 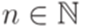 , что
, что 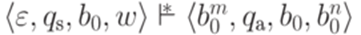 ;
;
2) для каждого слова 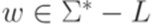 найдутся такие
найдутся такие 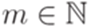 и
и 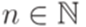 , что
, что 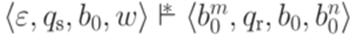 . Состояние qa называется допускающим (принимающим, accept state), состояние qr называется отвергающим (непринимающим, (reject state).
. Состояние qa называется допускающим (принимающим, accept state), состояние qr называется отвергающим (непринимающим, (reject state).
Пример 14.2.2. Рассмотрим детерминированную машину Тьюринга
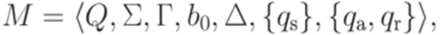
где 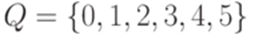 ,
, 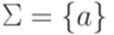 ,
, 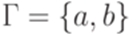 ,
,  ,
, 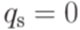 ,
,  ,
,  и
и
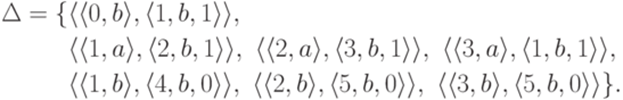
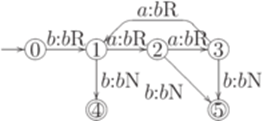
Эта машина Тьюринга разрешает язык 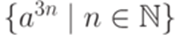 .
.
Определение 14.2.3. Язык L над алфавитом 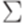 называется разрешимым или рекурсивным (decidable, recursive), если существует детерминированная машина Тьюринга
называется разрешимым или рекурсивным (decidable, recursive), если существует детерминированная машина Тьюринга
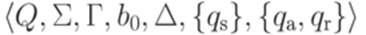
(с выделенным состоянием qa), которая разрешает язык L.
Определение 14.2.4. Говорят, что машина Тьюринга
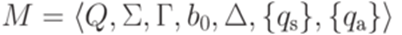
допускает (принимает, accepts) слово 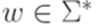 , если для некоторых
, если для некоторых 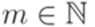 и
и 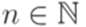
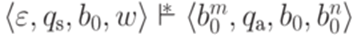 .
.
Определение 14.2.5. Язык, допускаемый машиной Тьюринга M, - это язык, состоящий из всех допускаемых данной машиной Тьюринга слов.
Определение 14.2.6. Язык называется перечислимым (рекурсивно перечислимым, полуразрешимым, recursively enumerable), если существует детерминированная машина Тьюринга, допускающая этот язык.
Замечание 14.2.7. В определении 14.2.6 можно отбросить требование детерминированности машины Тьюринга.
Теорема 14.2.8. Каждый разрешимый язык является перечислимым.
Доказательство. Пусть дана машина Тьюринга
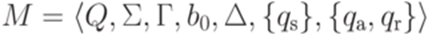
с выделенным состоянием qa, которая разрешает язык 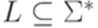 . Тогда машина Тьюринга
. Тогда машина Тьюринга
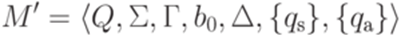
допускает язык L.
Пример 14.2.9. Если в машине Тьюринга из примера 14.1.15 заменить переход 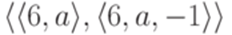 на
на 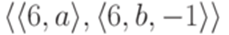 , то получится машина Тьюринга, допускающая язык
, то получится машина Тьюринга, допускающая язык 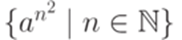 . Следовательно, этот язык является перечислимым. Можно доказать, что он даже является разрешимым.
. Следовательно, этот язык является перечислимым. Можно доказать, что он даже является разрешимым.
Теорема 14.2.10. Существует такая машина Тьюринга над однобуквенным алфавитом 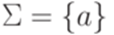 , что язык, допускаемый этой машиной Тьюринга, неразрешим.
, что язык, допускаемый этой машиной Тьюринга, неразрешим.
Доказательство. Доказательство существования перечислимого неразрешимого множества можно найти, например, в [31, 9.2].
Упражнение 14.2.11. Найти детерминированную машину Тьюринга с входным алфавитом {a}, разрешающую язык 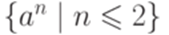 .
.
Упражнение 14.2.12. Найти детерминированную машину Тьюринга с входным алфавитом {a}, допускающую язык 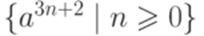
Массовые задачи
Определение 14.3.1. Массовой задачей (problem) называется бесконечная серия "однотипных" индивидуальных задач (instance), каждая из которых имеет определенный ответ. С каждой массовой задачей связана некоторая фиксированная схема кодирования (encoding scheme), которая отображает индивидуальные задачи в их коды - слова в некотором фиксированном алфавите. При этом требуется, чтобы множество кодов всех индивидуальных задач было разрешимым.
Определение 14.3.2. Задачей распознавания (decision problem) называется массовая задача, в которой ответами индивидуальных задач могут быть только "да" и "нет" (то есть существует только два возможных ответа).
Пример 14.3.3. Зафиксируем некоторый алфавит 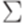 . Рассмотрим следующие однотипные индивидуальные задачи: даны два слова
. Рассмотрим следующие однотипные индивидуальные задачи: даны два слова 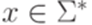 и
и 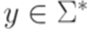 , необходимо выяснить, является ли слово x подсловом слова y.
, необходимо выяснить, является ли слово x подсловом слова y.
Пусть # - новый символ, не принадлежащий алфавиту 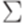 . Кодом индивидуальной задачи про конкретные слова x и yбудем считать слово x#y в алфавите
. Кодом индивидуальной задачи про конкретные слова x и yбудем считать слово x#y в алфавите 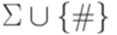 .
.
Эта массовая задача является задачей распознавания.
Определение 14.3.4. Алгоритмическая проблема - проблема, в которой требуется найти алгоритм для решения массовой задачи. Если такой алгоритм существует, то данная проблема называется алгоритмически разрешимой или просто разрешимой (decidable, solvable), в противном случае ее называют алгоритмически неразрешимой (undecidable, unsolvable).
Замечание 14.3.5. Алгоритмическая проблема, относящаяся к некоторой задаче распознавания, алгоритмически разрешима тогда и только тогда, когда разрешимо множество кодов индивидуальных задач с ответом "да".
Пример 14.3.6. Рассмотрим массовую задачу из примера 14.3.3. Соответствующая алгоритмическая проблема разрешима, так как разрешим язык 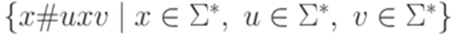 .
.
Пример 14.3.7. Зафиксируем некоторый алфавит 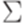 . Рассмотрим следующие однотипные индивидуальные задачи: дана порождающая грамматика
. Рассмотрим следующие однотипные индивидуальные задачи: дана порождающая грамматика
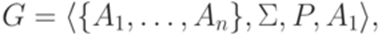
необходимо выяснить, является ли эта грамматика праволинейной.
Для полной строгости необходимо договориться, как кодировать грамматику G в виде слова. Например, можно использовать алфавит 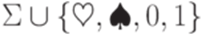 , где
, где  - дополнительные символы, не принадлежащие множеству
- дополнительные символы, не принадлежащие множеству 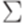 . Вспомогательный символ Ai заменим на слово, состоящее из символа
. Вспомогательный символ Ai заменим на слово, состоящее из символа  и кода числа i в двоичной системе счисления. В каждом правиле
и кода числа i в двоичной системе счисления. В каждом правиле  добавим символ
добавим символ  на месте
на месте  и после слова
и после слова 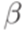 . Кодом грамматики G будем считать результат конкатенации кодов всех правил из множества P. Например, грамматика
. Кодом грамматики G будем считать результат конкатенации кодов всех правил из множества P. Например, грамматика
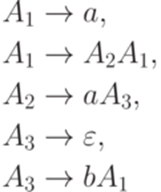
(над алфавитом 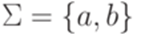 ) кодируется словом
) кодируется словом
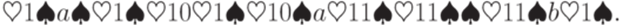
Легко понять, что соответствующая алгоритмическая проблема (проблема проверки праволинейности) разрешима.
Упражнение 14.3.8. Разрешима ли алгоритмическая проблема распознавания четности длины слова над алфавитом {a,b}?
14.4*. Грамматики типа 0
Теорема 14.4.1. Класс языков, порождаемых грамматиками типа 0, совпадает с классом перечислимых языков.
Доказательство можно найти, например, в [СерГал с. 24-26].
Упражнение 14.4.2. Выводимо ли слово aab в грамматике
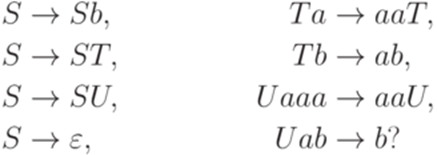
Упражнение 14.4.3. Выводимо ли слово aaaaaaaab в грамматике
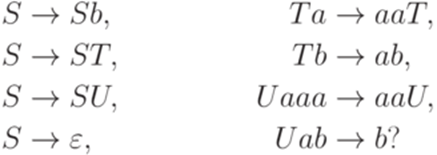
Замечание 14.4.4. Неизвестно, порождает ли грамматика

все слова в алфавите {a,b}.
Упражнение 14.4.5. Пусть 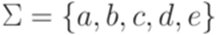 . Рассмотрим грамматику
. Рассмотрим грамматику

Выводимо ли в ней слово ccdcdcddccddcdcccabba?
Упражнение 14.4.6. Является ли разрешимым язык, порождаемый грамматикой
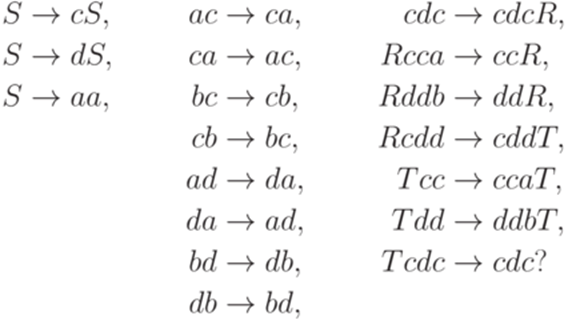
Определение 14.4.7. Порождающая грамматика в нормальной форме - это порождающая грамматика, в которой каждое правило имеет вид 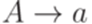 ,
, 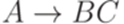 или
или 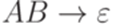 , где
, где 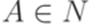 ,
, 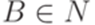 ,
, 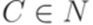 ,
, 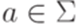 .
.
Теорема 14.4.8. Каждая порождающая грамматика эквивалентна некоторой порождающей грамматике в нормальной форме.
Упражнение 14.4.9. Существует ли такая порождающая грамматика G, что язык  не порождается ни одной грамматикой типа 0?
не порождается ни одной грамматикой типа 0?
 2020-05-25
2020-05-25 138
138








