Определение 16.5.1. Пусть  ,
,  ,
,  , где
, где 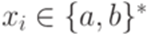 и
и 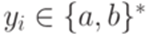 для всех i. Обозначим через
для всех i. Обозначим через  язык
язык  .
.
Лемма 16.5.2. Язык  является контекстно-свободным при любых
является контекстно-свободным при любых  и
и  .
.
Доказательство Утверждение следует из теорем 9.4.4 и 9.4.2.
Лемма 16.5.3. Рассмотрим алфавит  . Пусть
. Пусть  и
и  , где
, где  ,
,  и
и  для всех i. Тогда язык
для всех i. Тогда язык  является контекстно-свободным в том и только том случае, когда постовская система соответствия
является контекстно-свободным в том и только том случае, когда постовская система соответствия 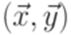 не имеет решений.
не имеет решений.
Доказательство. Пусть  - решение постовской системы соответствия
- решение постовской системы соответствия  , где
, где  для всех i. Положим
для всех i. Положим

Легко проверить, что  ,
,  и язык L0 является автоматным. Очевидно, что
и язык L0 является автоматным. Очевидно, что
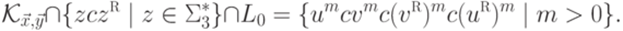
Можно доказать (например, используя лемму 9.1.1), что язык  не является контекстно-свободным. Согласно теореме 9.6.1 язык
не является контекстно-свободным. Согласно теореме 9.6.1 язык  также не~является контекстно-свободным.
также не~является контекстно-свободным.
Обратно, если постовская система соответствия 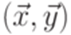 не имеет решений, то
не имеет решений, то  .
.
Теорема 16.5.4. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом  узнать, является ли контекстно-свободным язык
узнать, является ли контекстно-свободным язык 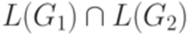 .
.
Доказательство. Достаточно построить по постовской системе соответствия 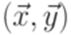 , где
, где  ,
,  и для всех i выполняется
и для всех i выполняется  ,
, 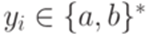 и
и  , контекстно-свободную грамматику G1, порождающую язык
, контекстно-свободную грамматику G1, порождающую язык  , и контекстно-свободную грамматику G2, порождающую язык
, и контекстно-свободную грамматику G2, порождающую язык  . С учетом леммы 16.5.3 неразрешимость рассматриваемой задачи сводится к неразрешимости проблемы соответствий Поста рассуждением, аналогичным приведенному в доказательстве теоремы 16.4.2.
. С учетом леммы 16.5.3 неразрешимость рассматриваемой задачи сводится к неразрешимости проблемы соответствий Поста рассуждением, аналогичным приведенному в доказательстве теоремы 16.4.2.
Лемма 16.5.5. Рассмотрим алфавит  . Язык
. Язык  является контекстно-свободным при любых
является контекстно-свободным при любых  и
и  .
.
Доказательство. Положим  . Язык
. Язык  можно представить в виде объединения пяти контекстно-свободных языков
можно представить в виде объединения пяти контекстно-свободных языков

Теорема 16.5.6. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной контекстно-свободной грамматике G над алфавитом  узнать, является ли контекстно-свободным язык
узнать, является ли контекстно-свободным язык  .
.
Доказательство. Рассмотрим алфавит  . Достаточно построить по постовской системе соответствия
. Достаточно построить по постовской системе соответствия  , где
, где  ,
,  и для всех i выполняется
и для всех i выполняется  ,
, 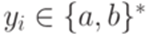 и
и  , контекстно-свободную грамматику G, порождающую язык
, контекстно-свободную грамматику G, порождающую язык 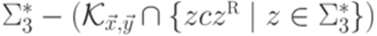 . С учетом леммы 16.5.5 неразрешимость рассматриваемой задачи сводится к~неразрешимости проблемы соответствий Поста рассуждением, аналогичным приведенному в доказательстве теоремы 16.4.2.
. С учетом леммы 16.5.5 неразрешимость рассматриваемой задачи сводится к~неразрешимости проблемы соответствий Поста рассуждением, аналогичным приведенному в доказательстве теоремы 16.4.2.
Лемма 16.5.7. Рассмотрим алфавит  . Язык
. Язык 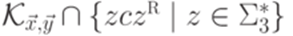 является контекстным при любых
является контекстным при любых  и
и  .
.
Теорема 16.5.8. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной контекстной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной контекстной грамматике G над алфавитом  узнать, является ли контекстно-свободным язык L(G).
узнать, является ли контекстно-свободным язык L(G).
Доказательство. Достаточно построить по постовской системе соответствия 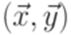 , где
, где  ,
,  и для всех i выполняется
и для всех i выполняется  ,
, 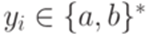 и
и  , контекстную грамматику G, порождающую язык
, контекстную грамматику G, порождающую язык 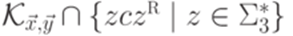 .
.
Упражнение 16.5.9. Является ли контекстно-свободным язык  , где язык L порождается грамматикой
, где язык L порождается грамматикой
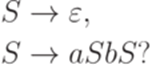
 2020-05-25
2020-05-25 120
120







