2020-05-21
154
Если колебательный контур (рис. 2.15) обладает активным сопротивлением R, то полная энергия контура с течением времени уменьшается вследствие выделения джоулева тепла на резисторе R при протекании через него тока. В таком контуре будут наблюдаться затухающие электромагнитные колебания.
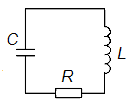
Рис. 2.15
Выведем уравнение затухающих электромагнитных колебаний. Изменение полной энергии контура за единицу времени равно выделяющейся тепловой мощности 
на сопротивлении R:
; (2.54)
. (2.55)
Учитывая, что 
, а 
; 
и, вводя обозначение
, (2.56)
получим
. (2.57)
Уравнение (2.57) является дифференциальным уравнением затухающих электромагнитных колебаний. Решением этого уравнения является функция, описывающая изменение заряда на обкладках конденсатора с течением времени:
|
|
|
, (2.58)
где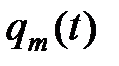 
– амплитуда колебаний заряда на обкладках конденсатора. С течением времени 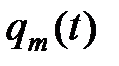убывает по экспоненциальному закону:
. (2.59)
Коэффициент затухания β, входящий в показатель экспоненты, характеризует быстроту уменьшения амплитуды колебаний, а частота 
затухающих колебаний связана с собственной частотой 
соотношением
(2.60)
На рис. 2.16 изображен график зависимости заряда на обкладках конденсатора от времени.
Рис. 2.16
Полная энергия колебательного контура уменьшается со временем по закону:
. (2.61)
Как видно из формул (2.21) и (2.61), энергия системы как в случае механических, так и электромагнитных затухающих колебаний убывает по экспоненциальному закону.
