СВОБОДНЫЕ СИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ
Понятие колебаний
Колебания – это периодический процесс, в котором значения какой-либо величины х точно или приближённо повторяются через равные промежутки времени Т, называемые периодом колебаний.
Существует много видов колебаний, например:
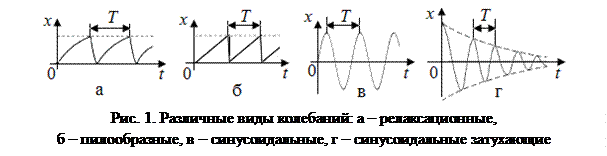
− релаксационные (рис. 1, а),
− пилообразные (рис. 1, б),
− синусоидальные (гармонические) незатухающие (рис. 1, в),
− синусоидальные затухающие (рис. 1, г).
Среди различных видов колебаний наиболее часто встречаются синусо-идальные (гармонические), описываемые функциями синуса или косинуса. По закону, близкому к синусоидальному, происходят колебания, например, в следующих механических системах:
а) шарик на зажатой с одного конца пружине (пружинный маятник),
б) шарик на нити (математический маятник),
в) любое твёрдое тело, которое может качаться в однородном поле тяжести на неподвижной горизонтальной оси (физический маятник),
г) натянутая струна,
д) столбики жидкости в U-образной трубке
Колебания называются свободными, если они происходят в первоначально выведенной из равновесия системе без дальнейшего поступления в нее энергии от внешних источников. Если же колебания в системе поддерживаются периодическим поступлением в нее энергии извне, то они называются вынужденными. Свободные колебания реальных механических (и электрических) систем всегда являются затухающими, т. е. с убывающей до нуля амплитудой. При этом первоначально запасенная колебательной системой энергия в конечном итоге превращается в тепло. Однако сначала для простоты удобно сначала рассмотреть идеализированный процесс незатухающих свободных колебаний, когда в системе отсутствует трение, приводящее к потерям (диссипации) энергии и убыванию амплитуды.
Уравнение свободных синусоидальных колебаний
Определение. Дифференциальное уравнение второго порядка вида
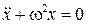 , (9.1)
, (9.1)
 где символом
где символом 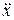 обозначена вторая производная по времени:
обозначена вторая производная по времени: 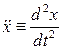 , называется уравнением свободных незатухающих синусоидальных (гармонических) колебаний. В этом уравнении х = х (t) – текущее смещение колеблющейся точки от положения равновесия, ω – параметр, называемый собственной частотой колебательной системы.
, называется уравнением свободных незатухающих синусоидальных (гармонических) колебаний. В этом уравнении х = х (t) – текущее смещение колеблющейся точки от положения равновесия, ω – параметр, называемый собственной частотой колебательной системы.
Уравнение (9.1) называется так потому, что его общим решением является функция
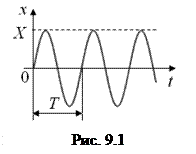
x (t) = X sin(ω t + φ), (9.2)
описывающая синусоидальный колебательный процесс с угловой частотой ω и амплитудой Х. Период таких колебаний Т = 2π / ω (рис. 9.1). Амплитуда Х – это максимальное отклонение от положения равновесия. Выражение (ω t + φ), стоящее под знаком синуса, называется фазой колебаний, а угловой параметр φ – начальной фазой. Угловая частота ω имеет размерность «рад/с». Прямой подстановкой легко проверить, что функция (9.2) действительно является общим решением уравнения (9.1), т. е. обращает его в тождество.
Значения параметров Х и φ в решении (9.2) определяются из начальных условий, т. е. из конкретного способа возбуждения колебаний. Эти конкретные способы будут рассмотрены в разделах 9.2 и 9.3.
Однако в дальнейшем общее решение уравнения (9.1) удобно представлять не в виде (9.2) а таком:
x (t) = А sin ω t +В cos ω t. (9.3)
Коэффициенты А и В здесь легко пересчитываются через Х и φ по известной формуле синуса суммы.
Если окажется, что движение какого-либо тела описывается дифференциальным уравнением вида (9.1), то это движение будет представлять собой синусоидальные колебания.
Простейшими идеализированными механическими колебательными системами, в которых могут происходить незатухающие колебания, являются маятники: пружинный, математический и физический. Рассмотрим эти три вида маятников по отдельности.
Пружинный маятник
Пусть груз массой m, лежащий на идеально гладкой горизонтальной плоскости, прикреплён к пружине жёсткостью k, которая другим концом закреплена на стенке (рис. 9.2, а). Очевидно, что если шарик вывести из положения равновесия и отпустить, то он будет совершать колебания. Поэтому такая колебательная система называется пружинным маятником. Покажем, что колебания груза в этом случае будут описываться уравнением (9.1).
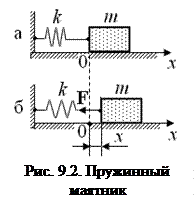 Проведём ось х как показано на рис 9.2, а, приняв х = 0 в точке равновесия груза. Выведем груз из равновесия, сдвинув его на небольшое расстояние х вправо, и затем отпустим. По закону Гука, на груз при этом будет действовать упругая сила Fx = − kx, направленная против смещения (рис. 9.2, б). Тогда, в силу 2-го закона Ньютона, уравнение движения груза будет таким:
Проведём ось х как показано на рис 9.2, а, приняв х = 0 в точке равновесия груза. Выведем груз из равновесия, сдвинув его на небольшое расстояние х вправо, и затем отпустим. По закону Гука, на груз при этом будет действовать упругая сила Fx = − kx, направленная против смещения (рис. 9.2, б). Тогда, в силу 2-го закона Ньютона, уравнение движения груза будет таким:
max = − kx,
или:
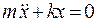 ,
,
или
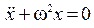 , (9.4)
, (9.4)
где символом ω2 обозначено отношение k/m, т. е.
ω = 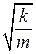 . (9.5)
. (9.5)
Видно, что уравнение движения груза (9.4) полностью совпадает с (9.1), следовательно, груз совершает синусоидальные колебания с угловой частотой (9.5). В общем виде эти колебания описываются функцией (9.3), в которой коэффициенты А и В определяются из начальных условий, т. е. из способа возбуждения колебаний груза. Начальными условиями для уравнения (9.4) являются значения координаты и скорости груза в начальный момент времени: х (0) и 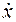 (0) = υ(0). Рассмотрим два типичных способа возбуждения колебаний груза: 1) груз оттянули и отпустили; 2) груз толкнули из положения равновесия.
(0) = υ(0). Рассмотрим два типичных способа возбуждения колебаний груза: 1) груз оттянули и отпустили; 2) груз толкнули из положения равновесия.
Вариант 1: груз оттянули вправо на заданное расстояние Х и отпустили. Тогда начальные условия запишутся так:
х (0) = Х, υ(0) = 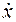 (0) = 0.
(0) = 0.
 Подставляя (9.3) в первое начальное условие, получаем:
Подставляя (9.3) в первое начальное условие, получаем:
А sin 0 + B cos 0 = Х,
откуда В = Х (коэффициент А пока не определён).
Подставляя (9.3) во второе начальное условие, получаем:
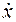 = А ω cos 0 – B ω sin 0 = А ω = 0,
= А ω cos 0 – B ω sin 0 = А ω = 0,
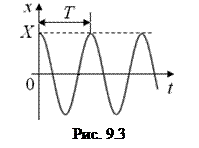
откуда А = 0. Таким образом, при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.3):
х = Х cos ω t. (9.6)
Вариант 2: груз толкнули из положения равновесия, т. е. в момент t = 0 при х = 0 ему сообщили начальную скорость υ0. В этом случае начальные условия будут иметь вид:
х (0) = 0, υ(0) = 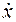 (0) = υ0.
(0) = υ0.
Подставляя (9.3) в первое начальное условие, получаем:
0 = А sin 0 + B cos 0,
откуда В = 0, т. е. теперь можно записать:
х = А sin ω t.
Подставляя это выражение во второе начальное условие, получаем:
υ0 = А ω cos 0,
т. е. А = υ0 / ω. И тогда при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.1):
х = Х sin ω t, (9.7) где 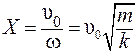 − амплитуда колебаний.
− амплитуда колебаний.
В обоих вариантах частота колебаний одна и та же (формула 9.5), и она определяется только массой груза и жёсткостью пружины. Период колебаний
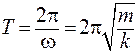 .
.
ПРИЛОЖЕНИЕ: закон Гука и энергия сжатой (растянутой) пружины.
Закон Гука утверждает, что для сжатия или растяжения пружины на величину х, к ней надо приложить силу F, пропорциональную х: F = kx. Коэффициент пропорциональности k называется жёсткостью пружины. Если к пружине прикреплено какое-то тело (груз), то на него со стороны деформированной пружины будет действовать сила, пропорциональная деформации х и противоположно направленная этой деформации: Fх = − kx (рис. 9.2,б).
Растягивая или сжимая пружину, сила F совершает работу
А = 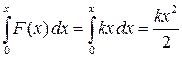 ,
,
в результате которой пружина приобретает потенциальную энергию
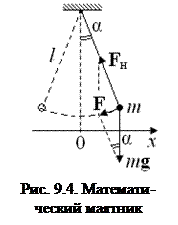 W =
W = 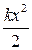 .
.
 2020-05-21
2020-05-21 411
411







