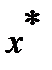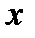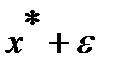| О |
| yb |
| b |
| у |
| х |
| В |
| Рис. 1. Брахистотрона |
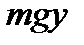 , где
, где 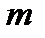 - масса точки,
- масса точки, 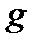 - ускорение свободного падения. Кинетическая энергия при этом увеличится на
- ускорение свободного падения. Кинетическая энергия при этом увеличится на 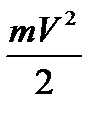 , где
, где 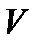 - скорость точки.
- скорость точки.
В силу закона сохранения энергии
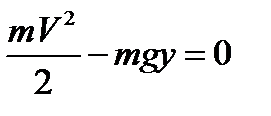 ,
,
откуда скорость точки 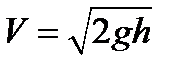 .
.
Предполагая, что траектория движения есть кривая, описываемая уравнением 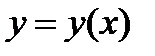 , причем
, причем  - гладкая функция, определенная на отрезке
- гладкая функция, определенная на отрезке 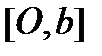 , получаем
, получаем
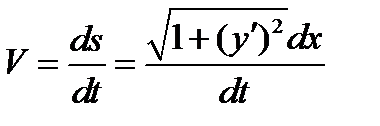 , (5)
, (5)
где: 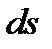 - дифференциал дуги кривой;
- дифференциал дуги кривой;
t – время.
Равенство (5) можно переписать в виде
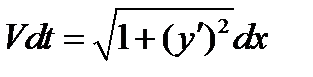 ,
,
откуда 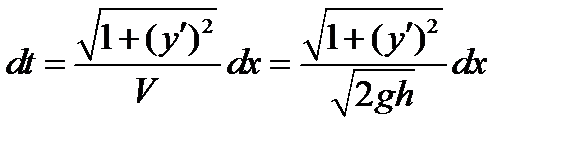 . (6)
. (6)
Используя уравнение (6), можно найти время, необходимое для перехода из точки О в точку В:
 . (7)
. (7)
Краевые условия
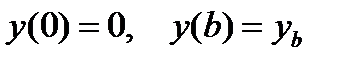 . (8)
. (8)
Требуется найти гладкую функцию  , доставляющую минимум интегралу (7) при краевых условиях (8).
, доставляющую минимум интегралу (7) при краевых условиях (8).
Задача о брахистотроне была сформулирована Иоганном Бернулли в 1696 году, поэтому1696 год принято считать датой рождения вариационного исчисления как раздела математики.
Основные определения
Пусть задано некоторое множество функций М.
Функционалом I на множестве М называется отображение 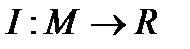 множества функций М на множество действительных чисел R.
множества функций М на множество действительных чисел R.
То есть функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если 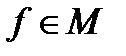 , то f - допустимая функция), областью значений функционала является множество действительных чисел. Т. е. функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если
, то f - допустимая функция), областью значений функционала является множество действительных чисел. Т. е. функционал – это функция, аргументами которой являются функции, принадлежащие некоторому множеству М (М – область определения функционала, если 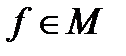 , то
, то  - допустимая функция), а областью значений функционала является множество действительных чисел.
- допустимая функция), а областью значений функционала является множество действительных чисел.
Множество М – нормированное пространство. Норма элемента 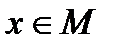 обозначается
обозначается 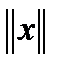 .
.
Нормой элемента 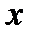 , принадлежащего некоторому пространству, называется вычисляемое по определенному правилу неотрицательное число, удовлетворяющее следующим свойствам:
, принадлежащего некоторому пространству, называется вычисляемое по определенному правилу неотрицательное число, удовлетворяющее следующим свойствам:
1). 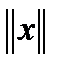 ≥ 0,
≥ 0, 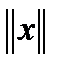 = 0 тогда и только тогда, когда x = 0.
= 0 тогда и только тогда, когда x = 0.
2). 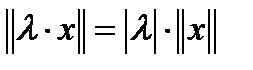 , где
, где 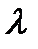 - число.
- число.
3). 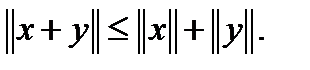
Примеры норм:
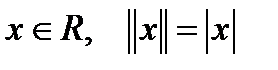
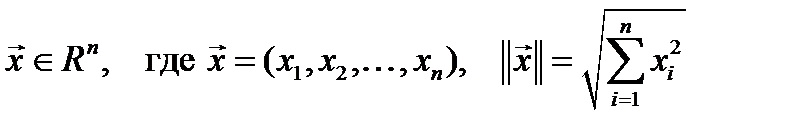 - евклидова норма. (9)
- евклидова норма. (9)
Пространство 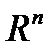 с заданной на нем нормой (9) называется евклидовым пространством.
с заданной на нем нормой (9) называется евклидовым пространством.
Если М – множество функций 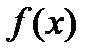 , непрерывных на отрезке
, непрерывных на отрезке 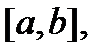 то для любой функции
то для любой функции 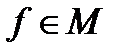 норма определяется формулой
норма определяется формулой
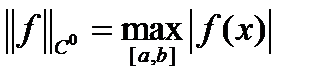 - банахова норма. (10)
- банахова норма. (10)
Если на множестве М функций, непрерывных на 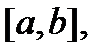 задана банахова норма (10), то М – банахово пространство
задана банахова норма (10), то М – банахово пространство 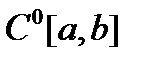 .
.
Если М – множество функций, непрерывных вместе со своими первыми производными на 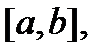 то это банахово пространство
то это банахово пространство  с нормой
с нормой
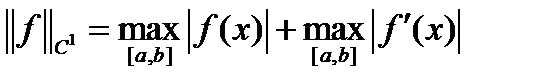 . (11)
. (11)
В общем виде: банахово пространство 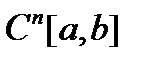 n раз непрерывно дифференцируемых на
n раз непрерывно дифференцируемых на 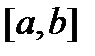 функций имеет норму, определяемую по формуле
функций имеет норму, определяемую по формуле
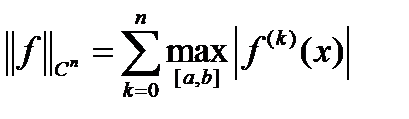 . (12)
. (12)
Значение аргумента действительной функции действительного аргумента 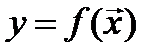 , где
, где 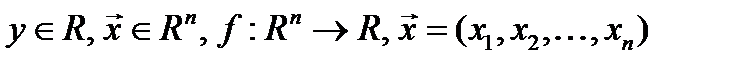 , называют точкой в пространстве
, называют точкой в пространстве 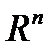 .
.
Расстояние между точками в евклидовом пространстве 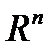 определяется нормой (9)
определяется нормой (9)
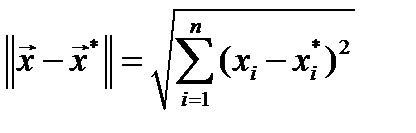 .
.
По аналогии функции, являющиеся аргументами функционала, мы будем называть точками в банаховом пространстве, а расстояния между функциями вычислять по формулам (10), (11) или (12).
Линейным функционалом называется функционал, удовлетворяющий условиям:
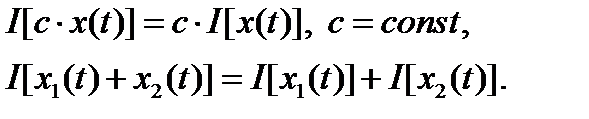 (13)
(13)
Пример:

Пусть задано произвольное положительное число 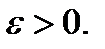
Сильной 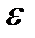 - окрестностью функции
- окрестностью функции 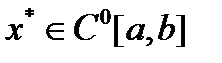 называется множество функций
называется множество функций 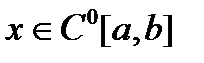 , для которых
, для которых 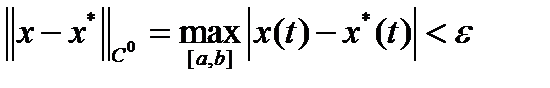 .
.
Слабой 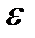 - окрестностью функции
- окрестностью функции 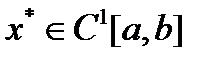 называется множество функций
называется множество функций 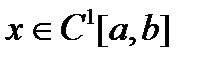 , для которых
, для которых 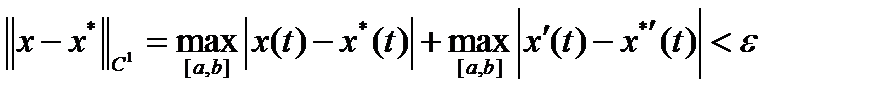 .
.
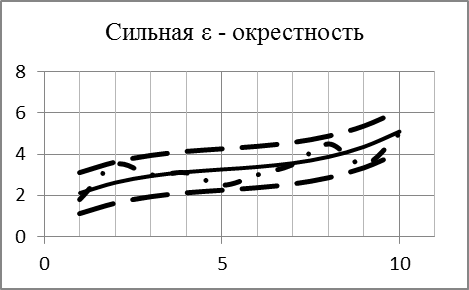
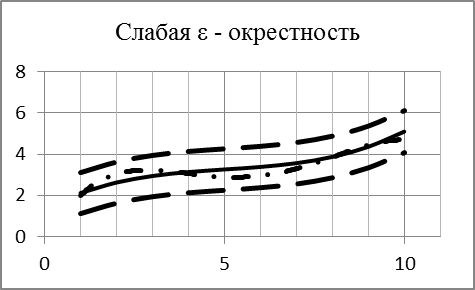
Графическая иллюстрация понятий сильной и слабой 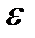 - окрестности функции показана на рисунке 2.
- окрестности функции показана на рисунке 2.
|
|
Рис. 2. e - окрестности функции.
Из определения e - окрестностей ясно, что функция, попадающая в слабую e - окрестность, принадлежит и сильной e - окрестности.
Функционал  , определенный на нормированном пространстве М, называется непрерывным в точке
, определенный на нормированном пространстве М, называется непрерывным в точке 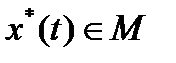 , если
, если
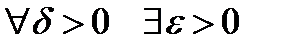 такое, что
такое, что 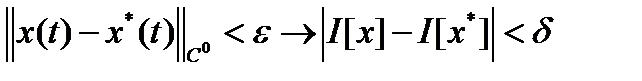 .
.
Выберем некоторую функцию 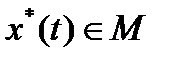 . Пусть
. Пусть 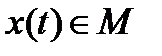 - произвольная функция.
- произвольная функция.
Разность
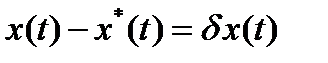 (14)
(14)
называется вариацией функции 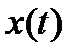 .
.
Отличие вариации функции 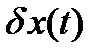 от приращения функции
от приращения функции 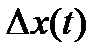 : приращение функции
: приращение функции 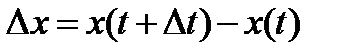 есть разность двух значений функции, то есть
есть разность двух значений функции, то есть 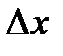 - число, а вариация
- число, а вариация 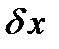 - функция,
- функция, 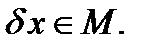
Приращением функционала 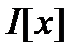 , определенного на нормированном пространстве
, определенного на нормированном пространстве 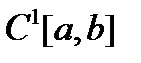 , в точке
, в точке 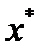 называется величина, вычисляемая по формуле
называется величина, вычисляемая по формуле
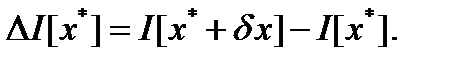
Вариации функционала
Если приращение функционала можно представить в виде
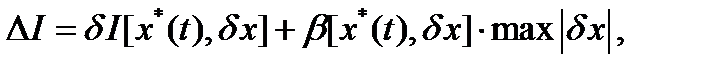
где 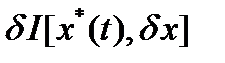 - линейный относительно
- линейный относительно 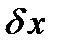 функционал,
функционал, 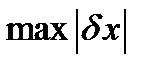 - максимальное значение
- максимальное значение 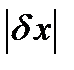 и
и 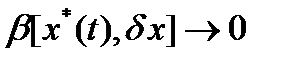 при
при 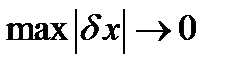 , то линейная по отношению к
, то линейная по отношению к 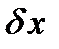 часть функционала
часть функционала 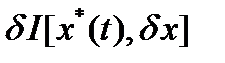 называется первой вариацией функционала.
называется первой вариацией функционала.
Можно дать и другое определение первой вариации функционала, используя представление функции 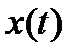 с использованием формулы (14):
с использованием формулы (14):
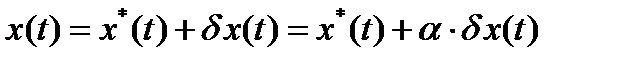 . (15)
. (15)
В формуле (15) вариация функции представлена как 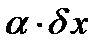 , где
, где 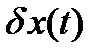 - фиксированная функция, а a - числовой параметр (переменная величина).
- фиксированная функция, а a - числовой параметр (переменная величина).
При таком представлении вариации функции выражение 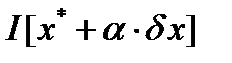 является функцией
является функцией 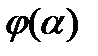 числового параметра a, поэтому ее можно разложить в ряд Тейлора по степеням a в окрестности точки a = 0:
числового параметра a, поэтому ее можно разложить в ряд Тейлора по степеням a в окрестности точки a = 0:
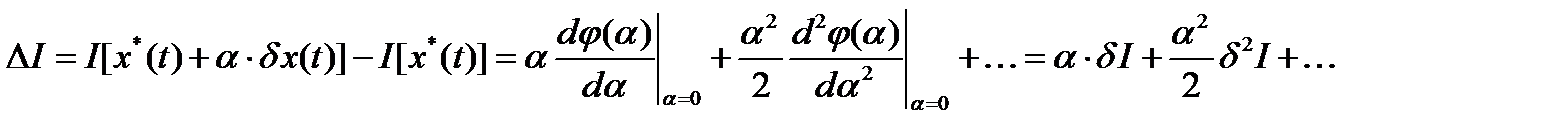
где: 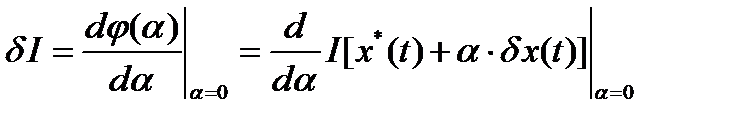 - первая вариация функционала,
- первая вариация функционала,
 - вторая вариация функционала.
- вторая вариация функционала.
Замечание. В литературе часто вместо обозначения 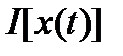 используют обозначение
используют обозначение 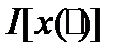 , чтобы отличать элемент
, чтобы отличать элемент 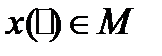 (то есть функцию, являющуюся точкой в некотором пространстве М) от значения функции
(то есть функцию, являющуюся точкой в некотором пространстве М) от значения функции 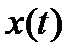 при фиксированном значении t (в этом случае
при фиксированном значении t (в этом случае 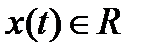 ).
).
Пример. Найти первую вариацию функционала
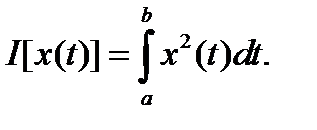
Первый способ.
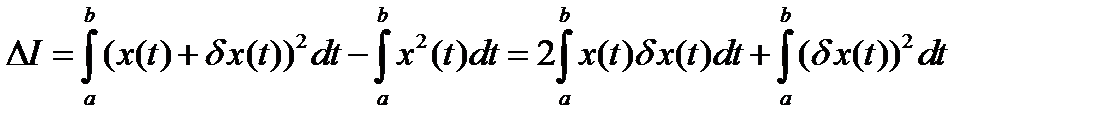 (16)
(16)
Для второго слагаемого в формуле (16) можно получить оценку сверху
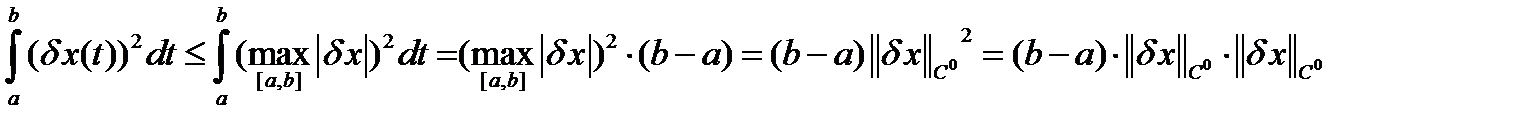 . (17)
. (17)
Подставляя (17) в формулу (16), получаем:
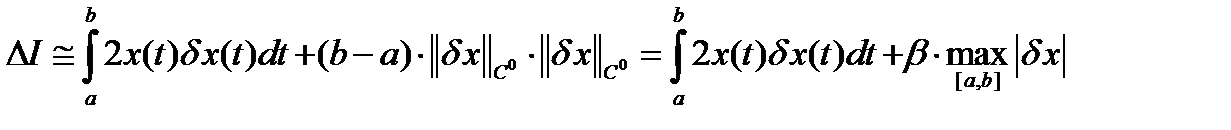 , (18)
, (18)
где  а первое слагаемое в формуле (18) линейно по
а первое слагаемое в формуле (18) линейно по 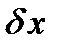 , следовательно, по определению первая вариация функционала равна
, следовательно, по определению первая вариация функционала равна
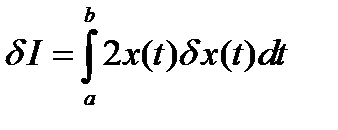 . (19)
. (19)
Второй способ.

В соответствии со вторым определением, первая вариация функционала равна
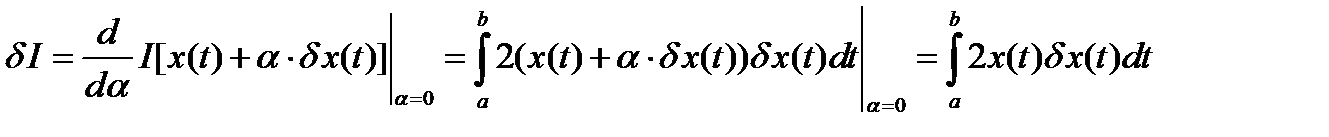 (20)
(20)
Сравнение (19) и (20) показывает, что оба способа вычисления первой вариации функционала дают одинаковый результат.
 2020-05-25
2020-05-25 234
234