Простейшие случаи интегрируемости уравнения Эйлера

a. Функция  не зависит явно от х, то есть . Уравнение Эйлера принимает вид , и, следовательно, . Это уравнение называется первым интегралом уравнения Эйлера.

b. Функция  не зависит явно от t и х, то есть . Уравнение Эйлера записывается в виде . Его общее решение имеет вид , а условие дает ОДУ первого порядка.

c. Функция  не зависит явно от t и , то есть , или не зависит явно от , то есть . Задача поиска экстремума в общем случае решения не имеет, т.к. уравнение Эйлера принимает вид  и не является дифференциальным, т.е. не содержит произвольных постоянных интегрирования и, вообще говоря, поэтому не удовлетворяет граничным условиям. Однако, если в частном случае решение уравнения проходит через граничные точки х₀, х₁, то экстремаль существует.

d. Подынтегральная функция имеет вид . Уравнение Эйлера в этом случае записывается в форме

Это уравнение не является дифференциальным. Если его решение удовлетворяет граничным условиям, то экстремаль существует. Если , то решения нет.

e. Функция  не зависит явно от t, то есть . Уравнение Эйлера в этом случае имеет вид:

f. .

Если это уравнение умножить на 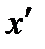, то его можно преобразовать к виду

g.  

Полученное ДУ имеет первый интеграл .