Алгоритм применения необходимых условий экстремума в зачах с фиксированными границами

1. Найти 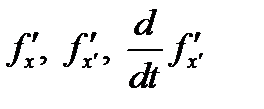 и записать уравнение Эйлера 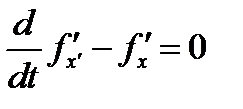. Если функция соответствует одному из простейших случаев интегрируемости, можно использовать уравнения, полученные в пунктах 2.5.2 a - 2.5.2 e.

2. Найти общее решение уравнения Эйлера 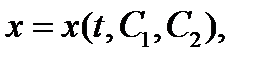 где С₁ и С₂ – произвольные постоянные.

3. Определить постоянные С₁ и С₂ из граничных условий:

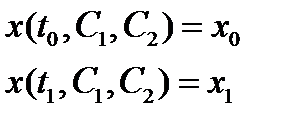
Пример. Найти экстремаль функционала

,

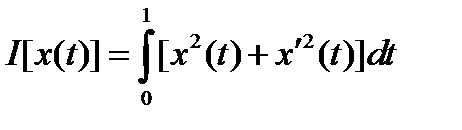удовлетворяющую граничным условиям х (0) = 0, х (1) =1.

Решаем задачу по алгоритму (п. 2.5.3.).

1. Найдем 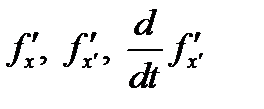: 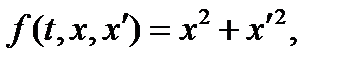следовательно, .

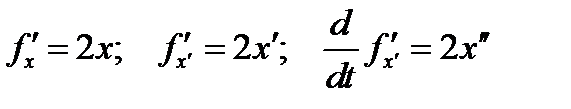Уравнение Эйлера 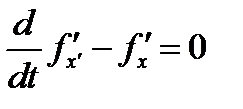 для данной задачи имеет вид 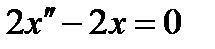, или, после сокращения на 2, .

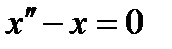2. Решение линейного ОДУ второго порядка ищем в виде 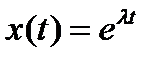. В результате подстановки 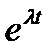в дифференциальное уравнение 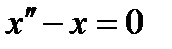получаем характеристическое уравнение

.

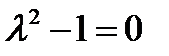Корни характеристического уравнения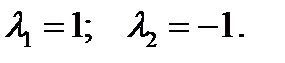  

Общее решение однородного уравнения

.

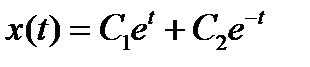3. Определяем постоянные С ₁ и С ₂ из граничных условий

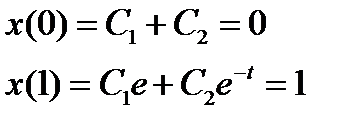
Получили систему двух уравнений с двумя неизвестными. Из первого уравнения следует 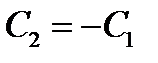. Поставляя полученное соотношение во второе уравнение, получаем 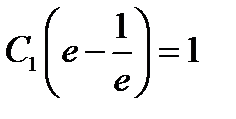, откуда следует .

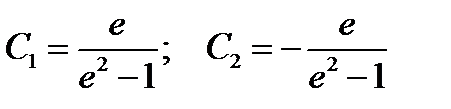Уравнение экстремали .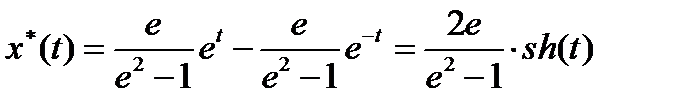

Оптимальное управление детерминированными системами