Раздел 16. Случайные величины
Дискретные и непрерывные случайные величины,
Способы их задания.
В результате двух последовательных подбрасываний одной монеты (или подбрасывании двух монет сразу) герб может появиться 0, 1 или 2 раза, т.е. в данном опыте число появлений герба будет случайным.
Определение. Случайной величиной называется величина, которая в результате опыта может принимать одно из своих возможных значений случайным образом.
Определение. Дискретной (прерывной) называется случайную величину, возможные значения которой есть отдельные изолированные числа. Число этих значений может быть конечным или бесконечным (счетным).
Определение. Законом распределения (рядом распределения) дискретной случайной величины  называется перечень ее возможных значений
называется перечень ее возможных значений  и соответствующих им вероятностей
и соответствующих им вероятностей  :
:

| 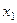
| 
| … | 
|

| 
| 
| … | 
|
Здесь  .
.
Закон распределения может быть также задан аналитически формулой  или с помощью функции распределения вероятностей
или с помощью функции распределения вероятностей
 .
.
Здесь суммируются вероятности  , отвечающие значениям
, отвечающие значениям 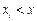 .
.
Закон распределения дискретной случайной величины можно изобразить графическ и, для чего в прямоугольной системе координат строят точки  ,
,  , …,
, …,  и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Определение. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно (сплошь) заполняют какой-то промежуток (числовой прямой).
Определение. Интегральной функцией или функцией распределения вероятностей непрерывной случайной величины  называется функция, определяемая равенством
называется функция, определяемая равенством
 .
.
Функция распределения (вероятностей) обладает свойствами:
1)  , 2)
, 2)  , если
, если  ,
,
2) 
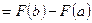 ,
,
3) 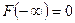 ,
,  .
.
В точках разрыва первого рода функция распределения  непрерывна слева:
непрерывна слева:  .
.
Определение. Дифференциальной функцией распределения или плотностью распределения вероятностей случайной величины  называется функция
называется функция
 .
.
Обратная связь между этими функциями определяется выражением
 .
.
Плотность распределения (вероятностей) обладает свойствами: 1)  , 2)
, 2)  (условие нормировки на единицу).
(условие нормировки на единицу).
Зная плотность распределения или функцию распределения, можно найти вероятность попадания непрерывной случайной величины  в интервал
в интервал  :
:

 .
.
16.2 Числовые характеристики случайной величины.
Закон распределения дискретной случайной величины  полностью задает эту величину. Иногда для общего представления о случайной величине достаточно ограничиться ее числовыми характеристиками, определяющими некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень разброса этих значений относительно среднего значения.
полностью задает эту величину. Иногда для общего представления о случайной величине достаточно ограничиться ее числовыми характеристиками, определяющими некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень разброса этих значений относительно среднего значения.
Определение. Математическим ожиданием дискретной случайной величины  называется число
называется число  , равное
, равное
 .
.
Если случайная величина  принимает счетное множество возможных значений, то математическое ожидание равно
принимает счетное множество возможных значений, то математическое ожидание равно

при условии, что этот ряд сходится абсолютно и  .
.
Для установления вероятностного смысла математического ожидания рассмотрим  испытаний, в результате которых случайная величина
испытаний, в результате которых случайная величина  принимает
принимает  раз значение
раз значение  ,
,  раз значение
раз значение  …,
…,  раз значение
раз значение  , причем
, причем  . Тогда среднее арифметическое значений, принятых значений равно
. Тогда среднее арифметическое значений, принятых значений равно

 .
.
Отсюда следует, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Поэтому часто математическое ожидание называют средним значением случайной величины.
Математическое ожидание обладает следующими свойствами:
1)  , где
, где  - неслучайная величина,
- неслучайная величина,
2) 
 ,
,
3) Для независимых случайных величин
 .
.
Если график плотности распределения вероятностей симметричен относительно прямой  , то
, то  .
.
Определение. Дисперсией случайной величины  называется математическое ожидание квадрата отклонения:
называется математическое ожидание квадрата отклонения:
 .
.
Для дискретной случайной величины дисперсия равна
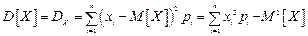 .
.
Отметим, что согласно определению дисперсии она неотрицательна и характеризует средний квадрат отклонения значений случайной величины от ее математического ожидания. Чем разброс этих значений больше, тем больше и дисперсия.
Дисперсия имеет следующие свойства:
1)  , где
, где  - неслучайная величина,
- неслучайная величина,
2)  ,
,
3) Для независимых случайных величин
 .
.
Определение. Средним квадратическим отклонением случайной величины  называется арифметическое значение квадратного корня из дисперсии:
называется арифметическое значение квадратного корня из дисперсии:
 .
.
Важной особенностью среднего квадратического отклонения является одинаковая с математическим ожиданием размерность, что не скажешь о дисперсии.
В случае непрерывной случайной величины  ее математическое ожидание и дисперсия рассчитываются с помощью формул
ее математическое ожидание и дисперсия рассчитываются с помощью формул
 ,
,
 .
.
Помимо рассмотренных числовых характеристик имеются и другие характеристики случайных величин, которые используются реже.
Определение. Начальным моментом 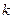 - го порядка называется число
- го порядка называется число
 .
.
Очевидно, что 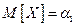 ,
,  .
.
Для дискретной случайной величины  начальный момент вычисляется по формуле
начальный момент вычисляется по формуле  , а для непрерывной случайной величины
, а для непрерывной случайной величины 
 .
.
Определение. Центральным моментом 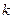 - го порядка называется число
- го порядка называется число
 .
.
Отсюда следует  ,
,  ,
,
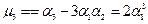 ,
,  .
.
Моменты более высоких порядков применяются редко.
Центральный момент 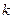 - го порядка дискретной случайной величины
- го порядка дискретной случайной величины  рассчитывается по формуле
рассчитывается по формуле
 .
.
В случае непрерывной случайной величины  имеем
имеем
 .
.
Если плотность распределения вероятностей случайной величины симметрично относительно ее математического ожидания, то все центральные моменты нечетного порядка равны нулю, т.е. 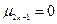 .
.
Определение. Коэффициентом ассиметрии распределения случайной величины  называется число
называется число 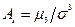 .
.
Ассиметрия положительна, если «длинная» часть кривой распределения расположена справа от математического ожидания, и наоборот.
Определение. Модой  непрерывной случайной величины называется ее возможной значение, соответствующее максимуму плотности распределения вероятностей.
непрерывной случайной величины называется ее возможной значение, соответствующее максимуму плотности распределения вероятностей.
Определение. Медианой  непрерывной случайной величины называется то ее возможное значение, которое определяется равенством
непрерывной случайной величины называется то ее возможное значение, которое определяется равенством  .
.
Основные случайные величины.
Далее рассмотрим случайные величины, наиболее часто встречающиеся в различных приложениях.
1. Равномерное распределение на множестве  .
.
Для этого распределения  с
с  . Математическое ожидание и дисперсия равны
. Математическое ожидание и дисперсия равны
 ,
,  .
.
Число очков, выпадающих на верхней грани игральной кости, является примером такой случайной величины, причем  ,
,  ,
, 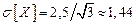
2. Биномиальное распределение.
Биномиальным называется закон распределения дискретной случайной величины  – числа появления события («успеха») в
– числа появления события («успеха») в  независимых испытаниях (опытах), в каждом из которых вероятность появления события равна
независимых испытаниях (опытах), в каждом из которых вероятность появления события равна 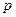 . Вероятность возможного значения
. Вероятность возможного значения  (
( ) вычисляется по формуле Бернулли:
) вычисляется по формуле Бернулли:
 .
.
Для этого распределения  ,
,  .
.
3. Распределение Пуассона.
Целочисленная случайная величина  , принимающая значения
, принимающая значения  , … имеет распределение Пуассона, если соответствующие вероятности задаются формулой Пуассона:
, … имеет распределение Пуассона, если соответствующие вероятности задаются формулой Пуассона:
 ,
,
где  и считается
и считается  .
.
Числовые характеристики равны  ,
,  .
.
Потоком событий называется последовательность событий, которые наступают в случайные моменты времени. Пуассоновским (простейшим) называется поток событий, обладающий следующими свойствами:
1) стационарность (вероятность появления 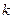 событий за промежуток времени
событий за промежуток времени  зависит только от
зависит только от 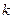 и
и  ),
),
2) отсутствие последействия (предыстория потока на влияет на вероятности появления событий в ближайшем будущем),
3) ординарность (вероятность появления более одного события за малый промежуток времени гораздо меньше вероятности появления только одного события).
Среднее число событий, которое появляется в единицу времени, называется интенсивностью потока  . Вероятность появления
. Вероятность появления 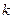 событий пуассоновского потока за время
событий пуассоновского потока за время  определяется формулой Пуассона
определяется формулой Пуассона
 .
.
4. Равномерное распределение на интервале  .
.
Непрерывная случайная величина  называется равномерно распределенной в интервале
называется равномерно распределенной в интервале  , если ее плотность распределения вероятностей равна
, если ее плотность распределения вероятностей равна

Функция распределения вероятностей равномерного распределения равна

Математическое ожидание и дисперсия равномерно распределенной непрерывной случайной величины равны
 ,
, 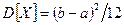 .
.
5. Показательное распределение.
Непрерывная случайная величина  называется распределенной по показательному закону, если ее плотность распределения вероятностей имеет вид
называется распределенной по показательному закону, если ее плотность распределения вероятностей имеет вид

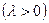 .
.
Функция распределения вероятностей показательного распределения равна

Математическое ожидание и дисперсия показательного распределения равны  ,
,  .
.
Длительность времени безотказной работы элемента некоторого устройства, имеющего интенсивность отказов  , часто имеет показательное распределение, функция распределения вероятностей которого
, часто имеет показательное распределение, функция распределения вероятностей которого 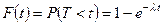
 равна вероятности отказа элемента за время длительностью
равна вероятности отказа элемента за время длительностью  .
.
Функция надежности  определяет вероятность безотказной работы элемента за время длительностью
определяет вероятность безотказной работы элемента за время длительностью  .
.
6. Нормальное распределение.
Непрерывная случайная величина 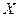 называется распределенной по нормальному закону или нормально распределенной, если ее плотность распределения вероятностей равна
называется распределенной по нормальному закону или нормально распределенной, если ее плотность распределения вероятностей равна


 ,
,
где 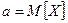 ,
,  .
.
Вероятность того, что нормально распределенная случайная величина 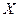 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  , равна
, равна
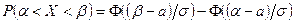 .
.
Здесь

– функция Лапласа, для которой 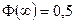 . Согласно равенству
. Согласно равенству  практически можно считать, что
практически можно считать, что  при
при 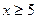 .
.
Вероятность того, что абсолютная величина отклонения  меньше положительного числа
меньше положительного числа  равна
равна
 .
.
При  отсюда следует правило «трех сигм»:
отсюда следует правило «трех сигм»:
 .
.
Определение. Эксцессом случайной величины 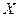 называется число
называется число  .
.
Для нормального распределения  . Если
. Если  , то кривая имеет более высокую и «острую» вершину, чем нормальная кривая.
, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая.
 2020-05-25
2020-05-25 175
175







