2020-05-25
132
Имеет место неравенство Маркова 
, из которого следует 
и далее неравенство Чебышева:
,
где 
- положительное число.
Неравенство Чебышева справедливо для любых случайных величин, имеющих дисперсию, не зависит от закона распределения случайной величины и может быть также представлено в виде
.
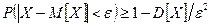Если 
- независимые случайные величины, то согласно неравенству Чебышева имеем неравенство
,
приводящее далее к теореме Чебышева.
Теорема (Закон больших чисел в форме Чебышева): Пусть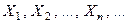 
– последовательность попарно независимых случайных величин, дисперсии которых ограничены одним и тем же числом 
: 
. Тогда для любого 
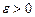при 
равномерно по 
.
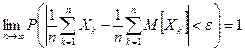Таким образом, среднее арифметическое случайных величин по вероятности сходится к среднему арифметическому их математических ожиданий.
Следствие. Среднее арифметическое последовательности попарно независимых величин, дисперсии которых ограничены и которые имеют одно и то же математическое ожидание 
, сходится по вероятности к математическому ожиданию , т. е. при любом положительном
|
|
|
.
Из теоремы Чебышева также следует теорема Бернулли.
Теорема Бернулли (закон больших чисел). Если в каждом из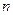 
независимых испытаний вероятность 
появления события 
постоянна, то относительная частота 
появлений события 
по вероятности стремится к , т.е. при любом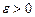
.
Также имеют место центральные предельные теоремы.
Теорема 1. Пусть 
- попарно независимые случайные величины, имеющие конечный третий абсолютный центральный момент 
, причем 
, 
, 
, 
, 
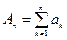. Если 
, то при равномерно по
.
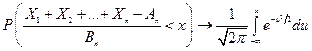Теорема 2. Пусть 
- попарно независимые случайные величины, имеющие конечное математическое ожидание 
и конечную дисперсию 
, тогда при 
равномерно по 
.
Следствие. Если - попарно независимые случайные величины, принимающие значение «1» с вероятностью 
и «0» с вероятностью 
, то при равномерно по 
,
где 
, 
, 
– число успехов в 
опытах.
Из данного следствия вытекают локальная и интегральная теоремы Муавра-Лапласа.
Пусть 
, тогда при для любого действительного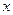 
согласно центральной предельной теореме
,
где 
– функция распределения вероятностей стандартного нормального закона.
Данная сходимость функции распределения вероятностей суммы независимых случайных величин к нормальному закону объясняет широкое применение этого закона на практике.
Например, при измерении некоторого параметра погрешность измерения может складываться из большого числа случайных слагаемых, вызываемых независимыми причинами и имеющими неизвестные законы распределения. Согласно центральной предельной теореме суммарная погрешность измерения имеет закон распределения, близкий к нормальному закону. Поэтому при измерениях часто результирующую погрешность измерений оценивают с помощью нормального закона. Обычно это делают уже при 
.
|
|
|
