Определение. Характеристической функцией одномерной случайной величины 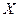 называется функция
называется функция
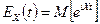 ,
,
где 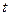 - действительная переменная,
- действительная переменная,  .
.
Для дискретной случайной величины характеристическая функция равна
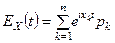 .
.
Непрерывная случайная величина 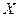 имеет характеристическую функцию
имеет характеристическую функцию
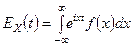 .
.
Для абсолютно интегрируемой характеристической функции 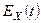 плотность распределения вероятностей равна
плотность распределения вероятностей равна
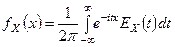 .
.
Характеристическая функция обладает следующими свойствами:
1) 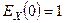 , 2)
, 2) 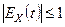 .
.
3) Если 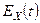 - характеристическая функция случайной величины
- характеристическая функция случайной величины 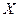 ,
, 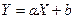 , то
, то 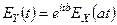 .
.
4) Если 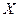 ,
, 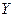 - независимые случайные величины, то
- независимые случайные величины, то
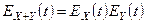 .
.
Характеристическая функция позволяет находить относительно просто начальные моменты произвольного порядка.
Теорема. Если случайная величина 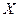 имеет начальный момент
имеет начальный момент 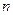 - го порядка, то ее характеристическая функция дифференцируема
- го порядка, то ее характеристическая функция дифференцируема 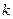 раз
раз 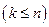 и
и 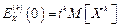 .
.
Введем функцию 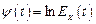 . Тогда
. Тогда
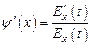 ,
, 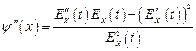
и, следовательно,
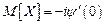 ,
, 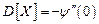 .
.
Определение. Производная 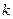 - го порядка логарифма характеристической функции в точке
- го порядка логарифма характеристической функции в точке 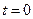 , умноженная на
, умноженная на 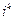 , называется семиинвариантом
, называется семиинвариантом 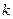 - го порядка случайной величины
- го порядка случайной величины 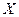 :
:

Для случайной величины, распределенной по нормальному закону, характеристическая функция равна
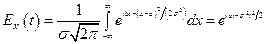 .
.
Случайная величина, распределенная по закону Пуассона, имеет характеристическую функцию
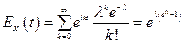 .
.
Для случайной величины, непрерывно распределенной на интервале 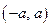 , характеристическая функция равна
, характеристическая функция равна
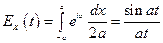 .
.
Для биномиального закона распределения характеристическая функция равна
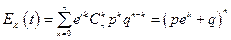 .
.
 2020-05-25
2020-05-25 201
201








