Пусть 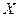 – дискретная случайная величина и
– дискретная случайная величина и  – монотонная функция, тогда
– монотонная функция, тогда  и
и  .
.
Если  – немонотонная функция, то для определения вероятности каждого возможного значения
– немонотонная функция, то для определения вероятности каждого возможного значения 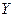 необходимо сложить вероятности всех возможных значений
необходимо сложить вероятности всех возможных значений 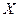 , при которых
, при которых  принимает это значение.
принимает это значение.
Пусть теперь 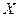 – непрерывная случайная величина с плотностью распределения вероятностей
– непрерывная случайная величина с плотностью распределения вероятностей  . Если
. Если  – непрерывная монотонно возрастающая функция, то существует однозначная обратная монотонно возрастающая функция
– непрерывная монотонно возрастающая функция, то существует однозначная обратная монотонно возрастающая функция  . В этом случае имеем
. В этом случае имеем
 .
.
 .
.
Для непрерывной монотонно убывающей функции  существует однозначная обратная монотонно убывающая функция
существует однозначная обратная монотонно убывающая функция  и, соответственно,
и, соответственно,

 ,
,
 .
.
.
Таким образом, если  - монотонная дифференцируемая функция, то, плотность распределения вероятностей случайной величины
- монотонная дифференцируемая функция, то, плотность распределения вероятностей случайной величины  определяется формулой
определяется формулой
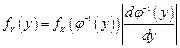 ,
,
где  – плотность распределения вероятностей случайной величины
– плотность распределения вероятностей случайной величины 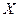 .
.
В случае немонотонной функции  интервал возможных значений
интервал возможных значений 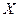 необходимо разбить на интервалы монотонности, найти плотности распределения вероятностей
необходимо разбить на интервалы монотонности, найти плотности распределения вероятностей  для каждого из интервалов монотонности и представить результирующую плотность распределения вероятностей в виде суммы
для каждого из интервалов монотонности и представить результирующую плотность распределения вероятностей в виде суммы
 .
.
Пример 1. Пусть  , тогда
, тогда
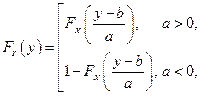 ,
, 
Для непрерывной случайной величины 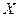 , распределенной по нормальному закону
, распределенной по нормальному закону 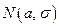 , случайная величина
, случайная величина  также будет распределена по нормальному закону:
также будет распределена по нормальному закону: 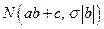 . Действительно,
. Действительно,
 Пример 2. Пусть
Пример 2. Пусть 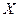 – непрерывная случайная величина,
– непрерывная случайная величина,  . В этом случае
. В этом случае  ,
,  при
при 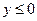 . Для
. Для  имеем
имеем

 .
.
Пусть 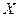 - нормально распределенная случайная величина со стандартным законом распределения
- нормально распределенная случайная величина со стандартным законом распределения  , тогда распределение случайной величины
, тогда распределение случайной величины  имеет вид
имеет вид
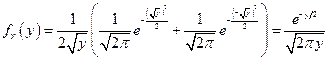 .
.
Пример 3 При моделировании технико-экономических показателей встречаются случайные величины, имеющие логарифмическое нормальное распределение. Найти это распределение.
Пусть  – случайная величина, распределенная по нормальному закону
– случайная величина, распределенная по нормальному закону 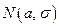 . Тогда
. Тогда  при
при 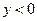 и
и
 ,
, 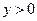 .
.
Числовые характеристики функции  случайного аргумента
случайного аргумента 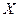 можно находить непосредственно, используя закон распределения аргумента
можно находить непосредственно, используя закон распределения аргумента 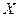 и формулы
и формулы
 ,
,  .
.
 2020-05-25
2020-05-25 257
257








