ОСНОВНЫЕ ФОРМУЛЫ
| Показатель преломления вещества и скорость света где n – показатель преломления; с – скорость света в вакууме; v - скорость света в среде; ε – диэлектрическая проницаемость среды; μ – магнитная проницаемость среды. |
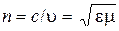 , ,
|
| Объемная плотность энергии электромагнитной волны где Е, Н – напряженности электрического и магнитного полей, ε0 и μ0 – электрическая и магнитная постоянные |
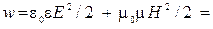 =
= 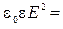 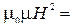 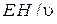
|
| Интенсивность волны < w > - среднее значение объемной плотности энергии |
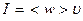
|
| Давление света на плоскую поверхность где α – угол падения волны на поверхность, R – коэффициент отражения |
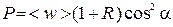 , ,
|
| Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой пленки, находящейся в воздухе где d – толщина пластинки, n – показатель преломления материала пластинки, a – угол падения, λ – длина волны. |
Δ = 2 d 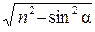 + l/ 2, + l/ 2,
|
| Радиус темных колец Ньютона при наблюдении в отраженном свете (светлых в проходящем свете) где R – радиус кривизны линзы, λ – длина волны, m = 1,2… |
r m = 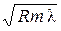 , ,
|
| Радиус светлых колец при наблюдении в отраженном свете (темных в проходящем свете) |
r m = 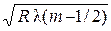 . .
|
| Радиус зоны Френеля где а, b – расстояния от препятствия (отверстия) до источника света и точки наблюдения соответственно, m = 1,2… | 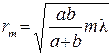
|
| Условие дифракционных минимумов на щели шириной а где φ – угол дифракции | a sin j = ± m l |
| Условие главных дифракционных максимумов на решетке с периодом d | d sin j = ± m l, |
| Условие главных дифракционных минимумов на решетке с периодом d = a + b | a sin j = ± m l, |
| Степень поляризации частично поляризованного света где Iп – интенсивность поляризованной компоненты излучения, I – полная интенсивность |
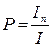 , ,
|
| Закон Малюса где φ – угол между плоскостью поляризации падающего света и главной плоскостью анализатора |
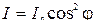 , ,
|
| Закон Брюстера где α Б - угол Брюстера | 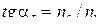
|
| Коэффициенты: - отражения - поглощения - пропускания вещества | 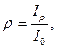
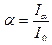
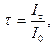
|
| Коэффициент отражения при нормальном падении пучка лучей | 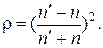
|
| Закон Бугера где a и а 10 – экспоненциальный и десятичный показатели поглощения среды, l – длина пути излучения в среде |
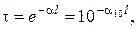
|
Закон Кирхгофа
где 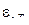 – спектральная плотность энергетической светимости абсолютно черного тела – спектральная плотность энергетической светимости абсолютно черного тела
| 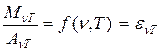
|
Закон Стефана-Больцмана
где 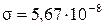 Вт/ м2К4,
Т - абсолютная температура Вт/ м2К4,
Т - абсолютная температура
|
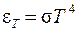
|
Закон смещения Вина
где  – длина волны, на которую приходится максимум – длина волны, на которую приходится максимум 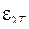 , b = 2,9 × 10 -3 м· К , b = 2,9 × 10 -3 м· К
|
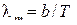
|
| Энергия фотона где h – постоянная Планка | ε = h ν = h c / λ |
| Импульс фотона | p = h ν/ c = h / λ |
| Уравнение Эйнштейна для внешнего фотоэффекта где h ν - энергия поглощенного фотона, А - работа выхода электрона, W K – максимальная кинетическая энергия фотоэлектрона | h ν = А + W K |
| Красная граница фотоэффекта | λ0 = h c / А |
| Световое давление, возникающее вследствие передачи фотонами импульса при соударении с преградой где N - число фотонов, падающих на единичную площадку в единицу времени, R – коэффициент отражения, α – угол падения света на поверхность | P = (1 + R) N (h ν / c) cos2α |
| Эффект Комптона где θ – угол рассеяния, λС = h / m 0 с - комптоновская длина волны | Δλ = λС (1 – cos θ), |
Взаимосвязь корпускулярных и волновых характеристик частицы
E-энергия, 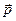 -импульс, ћω-энергия кванта, -импульс, ћω-энергия кванта, 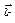 -волновой вектор -волновой вектор
| 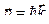 , E = ћω
p = h ν/ c = h /λ , E = ћω
p = h ν/ c = h /λ
|
| Соотношения неопределенностей | 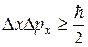 , , 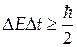
|
| ФормулаДе Бройля Волна Де Бройля | 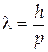
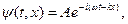 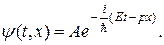 k= k= 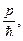 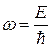
|
| Уравнение Шредингера Трехмерное уравнение Шредингера Оператор Лапласа Вероятность обнаружения частицы в объёме dV Условие нормировки |
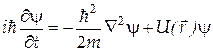
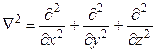 - -
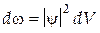
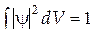
|
Стационарное уравнение Шредингера для функции  для трехмерного и для трехмерного и 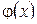 одномерного случаев.
Волновая функция стационарного состояния частицы одномерного случаев.
Волновая функция стационарного состояния частицы
| 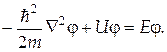
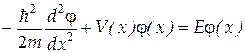
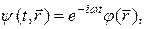
|
| Энергия частицы, внутри потенциальной ямы | 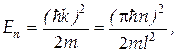 где n = 1, 2, 3,… где n = 1, 2, 3,…
|
| Волновая функция для частицы в потенциальной яме ширины l с бесконечно высокими стенками | φ (x) = A sin 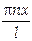 , , 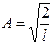
|
| Спектр энергий гармонического осциллятора | 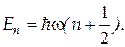 где n = 0,1, 2, 3,… где n = 0,1, 2, 3,…
|
| Коэффициенты D прохождения частицы через потенциальный барьер произвольной формы, где а и b - значения координаты х, при которых функция U(x) равна Е, и прямоугольный барьер шириной l. |
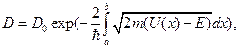
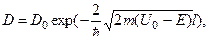 D 0 ≈ 1 D 0 ≈ 1
|
| Частоты излучения, которое могут испускать или поглощать атомы водорода Постоянная Ридберга R | ω = R (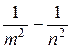 )
R = 2,07 · 1016 c -1 )
R = 2,07 · 1016 c -1
|
Модуль L вектора 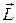 момента импульса электрона, момента импульса электрона,
| 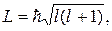 l = 0, 1, 2, …, n – 1,
где l -орбитальное квантовое число l = 0, 1, 2, …, n – 1,
где l -орбитальное квантовое число
|
| Проекция вектора L момента импульса электрона на заданное направление z в пространстве | L z = ħm, m = - l, - l + 1, …, -1, 0, 1,…, l – 1, l, где магнитное квантовое число |
| Радиус ядра | R = R 0 A 1/3, где Ro= 1,3 · 10-15 м. |
| Дефект массы ядра | Δ m = Zmp + Nmn - M. Eсв = (Z mp + N mn – M) c 2 = Δ m c 2 |
| Условная запись ядерной реакции: В качестве частиц а и b в ядерной реакции могут участвовать нейтрон n, протон р, ядро тяжелого водорода 21 Н - дейтон, α-частица или γ-квант. | X + a → Y + b, или X (a, b) Y |
| Энергия реакции самопроизвольного распада ядра X на два ядра Y 1и Y 2: X → Y 1+ Y 2. | Q = (M – (M 1 + M 2)) c 2 где М, M1 и М2 - массы ядер X, Y1 и Y 2 соответственно. |
| Энергии связи нуклонов в ядрах: | ECB(Z, A) = (Zmp + Nmn - Mz A) с2 |
| Закон ядерного распада | N (t) = N 0 e –λt |
| Соотношение для периода полураспада Т: | eλT = 2 |
 2020-05-21
2020-05-21 264
264








