2020-05-25
1214
При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:
допущение 1: поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли);
допущение 2: радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины;
допущение 3: длина вала в результате закручивания не изменяется.
Поперечное сечение вала ведет себя при кручении, как жесткий диск, и деформацию кручения можно рассматривать, как результатсдвига (скольжения)одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.
Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными. Одним из первых исследователей, изучавших кручение круглых стержней опытным путем, был Вертгейм.
Стержни прямоугольного поперечного сечения при кручении
Допущения, принятые для круглого вала, не могут быть приняты для стержня прямоугольного поперечного сечения. При кручении прямоугольного стержня отдельные точки поперечного сечения перемещаются вдоль его оси, и сечение перестает быть плоским. Происходит депланация поперечного сечения стержня.
Кручение стержней прямоугольного сечения значительно сложнее по сравнению со случаем стержня круглогопоперечногосечения, и методы сопромата не подходят для расчета прямоугольных стержней на кручение.
Зависимость между углом сдвига и относительным углом закручивания
Рассмотрим часть вала длиной 
. Правое поперечное сечение вала провернулось на угол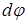 
относительно левого сечения. Для произвольного продольного волокна, отстоящего от оси вала на расстоянии 
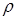, возникнет абсолютный сдвиг, равный 
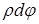(рис. 5.1).
Формула угла сдвига имеет вид:
.
Входящая в формулу угла сдвига величина 
называется относительным углом закручивания.
Таким образом, существует зависимость между углом сдвига и относительным углом закручивания:
.
Закон Гука при кручении
Закон Гука при кручении записывается, как закон Гука при сдвиге:
,
Формула закона Гука при кручении с учетом зависимости между углом сдвига и относительным углом закручивания:
Формулировка закона Гука при кручении: касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести на расстоянии 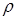, пропорциональны относительному углу закручивания. В точках, равноудаленных от центра тяжести сечения, численные значения касательных напряжений одинаковы.
Из формулы закона Гука при кручении следует: касательные напряжения в поперечном сечении вала изменяются по линейному закону (пропорционально расстоянию от точки до центра тяжести). Касательные напряжения равны нулю в центре вала и достигают максимального значения (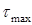
) в точках контура поперечного сечения (рис. 5.2).
Из рис. 5.2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полые валы. Такие валы, при той же площади поперечного сечения (F), могут воспринять больший скручивающий момент.
Касательные напряжения в произвольной точке поперечного сечения вала. Максимальные касательные напряжения при кручении
Подставив выражение 
в формулу получим формулу касательных напряжений сечения вала в любой точке поперечного сечения вала:
Наибольшие касательные напряжения (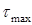) возникают в точках контура поперечного сечения при 
.
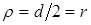Формула наибольших касательных напряжений:
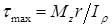
Введя обозначение 
, окончательно получим формулу максимальных касательных напряжений в сечении вала:
, где Wp – полярный момент сопротивления.
