| Номер схемы | М1, кН·м | М2, кН·м | М3, кН·м | М4, кН·м | a, м | b, м | c, м | d, м |
| 1 | 1,0 | 2,0 | 1,0 | 1,0 | 1,0 | 1,2 | 1,4 | 1,6 |
| 2 | 1,0 | 2,0 | 1,0 | 0,8 | 1,2 | 1,4 | 1,6 | 1,9 |
| 3 | 2,0 | 4,0 | 1,0 | 1,0 | 1,4 | 1,6 | 1,0 | 1,2 |
| 4 | 3,0 | 5,0 | 1,6 | 1,4 | 1,6 | 1,0 | 1,2 | 1,4 |
| 5 | 4,0 | 6,0 | 1,8 | 1,4 | 1,1 | 1,1 | 1,8 | 1,5 |
| 6 | 2,0 | 4,0 | 1,2 | 1,2 | 1,3 | 1,3 | 1,5 | 1,1 |
| 7 | 2,0 | 3,0 | 1,2 | 1,0 | 1,5 | 1,5 | 1,3 | 1,3 |
| 8 | 3,0 | 4,0 | 1,0 | 1,0 | 1,7 | 1,7 | 1,5 | 1,4 |
| 9 | 4,0 | 5,0 | 1,8 | 1,6 | 1,9 | 1,9 | 1,7 | 1,3 |
| 0 | 5,0 | 6,0 | 2,0 | 1,6 | 1,2 | 1,4 | 1,4 | 1,2 |
Решение задач по сопромату рекомендуется производить по правилам:
1. Перед решением задачи по сопромату необходимо переписать полностью ее условие с числовыми данными, составить эскиз в масштабе и указать на нем в числах все величины, необходимые для дальнейшего расчета,
2. Решение задач по сопромату дополняйте краткими пояснениями и чертежами, на которых визуализированы входящие в расчет величины,
3. Перед использованием формулы для определения напряженно-деформированного состояния необходимо изучить соответствующую тему лекций по сопромату, чтобы понять физический смысл всех величин, входящих в нее,
|
|
|
4. При подстановке в используемую формулу величин силы, момента или длины необходимо перевести их в одну систему единиц,
5. При решении задач по сопромату точность расчетов не должна превышать трех значащих цифр (результат решения задачи не может быть точнее заложенных в расчетные формулы предпосылок),
6. Заканчивать расчеты нужно анализом результатов - преподавали по сопромату таким образом проверяют ваши работы. Анализ результатов решения поможет избежать нелепых ошибок и оперативно их устранить.
Варианты расчетных схем к задаче на кручение стержня круглого сечения для самостоятельного решения bervengas@inbox.ru
Что такое кручение?
Эпюра крутящих моментов
Скручивающий момент формула
Допущения теории круглых стержней
Прямоугольный стержень кручение
Угол сдвига формула
Закон Гука при кручении
Крутящий момент через касательные напряжения формула
Угол закручивания и крутящий момент формула
Касательные напряжения сечения вала формула
Полярный момент сопротивления
Условие прочности кручение формула
Условие жесткости кручении
Потенциальная энергия кручение формула
Пример решения задачи по теме "геометрические характеристики плоских сечений"
Условие в примере решения задачи "геометрические характеристики плоских сечения"
Для составного поперечного сечения стержня, состоящего из равнобокого уголка № 7 с толщиной стенки 8 мм, швеллера № 22 и полосы 180´20 мм (рис. 3.10), требуется найти положение центра тяжести сечения, направление главных центральных осей инерции u и v, а также вычислить главные центральные моменты инерции 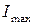 и
и  .
.
|
|
|
Расчетная схема к примеру решения задачи "геометрические характеристики плоских сечений"
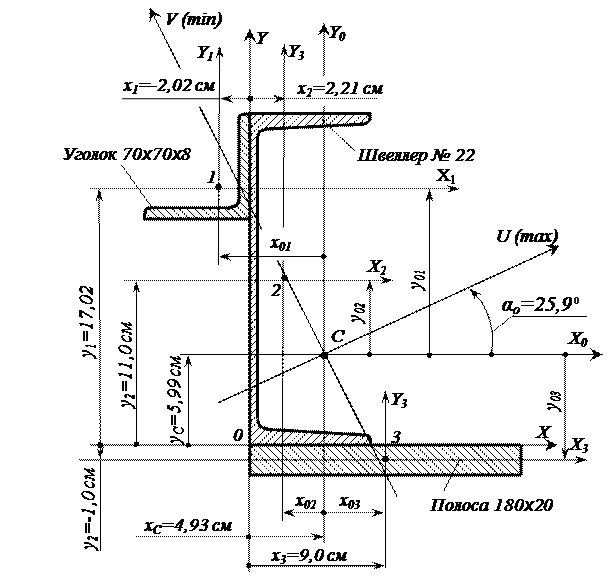
Решение примера задачи "геометрические характеристики плоских сечений"
Определяем координаты центра тяжести поперечного сечения
Размеры и геометрические характеристики уголка и швеллера устанавливаем по сортаментам (прил. 1, табл. П1.1, П1.4). Вычерчиваем сечение в масштабе (см. рис. 3.10). Выбираем оси сравнения 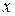 и
и 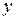 , располагая их по контуру швеллера. Именно в этих осях мы и будем определять положение центра тяжести всего сечения. Для каждого элемента сечения (уголка, швеллера и полосы) проводим собственные центральные оси
, располагая их по контуру швеллера. Именно в этих осях мы и будем определять положение центра тяжести всего сечения. Для каждого элемента сечения (уголка, швеллера и полосы) проводим собственные центральные оси 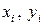 (
(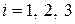 ), параллельные выбранным осям сравнения
), параллельные выбранным осям сравнения 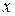 и
и 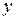 .
.
Координаты центра тяжести всего поперечного сечения (точка С), состоящего из трех элементов (уголка – 1, швеллера – 2 и полосы – 3), вычисляются по формулам:
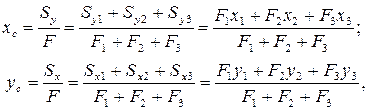
где  и
и 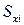 – статические моменты соответствующего элемента относительно осей сравнения;
– статические моменты соответствующего элемента относительно осей сравнения; 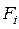 – площадь элемента;
– площадь элемента; 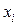 и
и 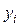 – координаты центра тяжести элемента
– координаты центра тяжести элемента 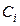 в осях сравнения. Вычисления производим в табличной форме (табл. 3.6).
в осях сравнения. Вычисления производим в табличной форме (табл. 3.6).
Таблица 3.6
Определение координат центра тяжести поперечного сечения
| Номер элемента | Наименование элемента | Площадь элемента
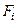 , см2 , см2
| Координаты
центра тяжести элемента 
| Статические моменты
элемента относительно осей сравнения 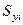 и и 
| ||
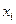 , см , см
| 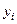 , см , см
|  , см3 , см3
|  , см3 , см3
| |||
| 1 | Уголок | 10,67 | -2,02 | 17,02 | -21,55 | 181,60 |
| 2 | Швеллер | 26,70 | 2,21 | 11,00 | 59,01 | 293,70 |
| 3 | Полоса | 36,00 | 9,00 | -1,00 | 324,00 | -36,00 |
| S | Все сечение | 73,37 | 361,46 | 439,30 |
Координаты центра тяжести поперечного сечения (точка С) в осях сравнения 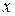 ,
, 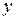 :
:
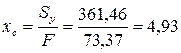 см;
см; 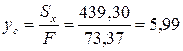 см.
см.
По найденным значениям 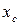 и
и 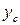 отмечаем на чертеже центр тяжести всего сечения точку С (см. рис. 3.10) и проводим центральные оси
отмечаем на чертеже центр тяжести всего сечения точку С (см. рис. 3.10) и проводим центральные оси 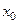 и
и  .
.
Заметим, что центр тяжести всей фигуры должен располагаться внутри треугольника, вершинами которого являются центры тяжести элементов поперечного сечения.
Вычисляем моменты инерции всего поперечного сеченияотносительно центральных осей 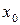 и
и 
Осевые и центробежный моменты инерции сечения относительно центральных осей определяются по следующим формулам:
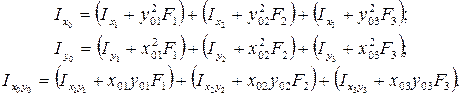
Значения осевых моментов инерции уголка 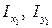 и швеллера
и швеллера 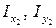 относительно собственных центральных осей
относительно собственных центральных осей 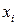 и
и 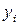 определяем по сортаменту (см. прил. 1). Для полосы осевые моменты инерции соответственно равны:
определяем по сортаменту (см. прил. 1). Для полосы осевые моменты инерции соответственно равны:

 см4;
см4; 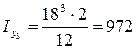 см4.
см4.
Центробежные моменты инерции швеллера  и полосы
и полосы 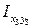 равны нулю, поскольку их собственные центральные оси являются осями симметрии.
равны нулю, поскольку их собственные центральные оси являются осями симметрии.
Центробежный момент инерции уголка 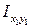 относительно собственных центральных осей
относительно собственных центральных осей 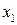 и
и  вычисляется по формуле
вычисляется по формуле
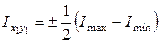 ,
,
где 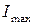 и
и  – максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что
– максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что 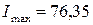 см4, а
см4, а  см4.
см4.
Центробежный момент инерции уголка не равен нулю, поскольку оси 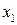 и
и  не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей
не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей 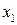 и
и  на угол 450).
на угол 450).
Знак центробежного момента инерции уголка (как, впрочем, и для любой другой фигуры) зависит от направления координатных осей. Он легко определяется следующим образом. Согласно определению, центробежный момент инерции фигуры равен интегралу, в котором элементарная площадка  умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,
умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,
|
|
|
 см4.
см4.
Теперь определяем координаты центров тяжести отдельных элементов 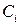 в центральных осях
в центральных осях 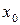 и
и  :
:
для уголка
 см;
см;
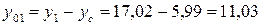 см;
см;
для швеллера
 см;
см;
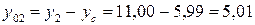 см;
см;
для полосы
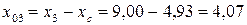 см;
см;
 см.
см.
Дальнейшие вычисления моментов инерции всего поперечного сечения относительно центральных осей 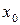 и
и  производим в табличной форме (табл. 3.7).
производим в табличной форме (табл. 3.7).
Таблица 3.7
Определение моментов инерции сечения относительно
центральных осей 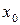 и
и 
| Номер элемента | Наименование элемента | Площадь элемента 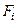 , см2 , см2
| Моменты инерции относительно собственных центральных осей 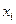 и и 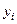
| Координаты
центра тяжести в осях 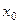 и и 
| |||
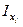 , см4 , см4
| 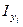 , см4 , см4
| 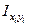 , см4 , см4
| 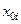 , см , см
| 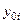 , см , см
| |||
| 1 | Уголок | 10,67 | 48,16 | 48,16 | 28,19 | -6,95 | 11,03 |
| 2 | Швеллер | 26,70 | 2110,00 | 151,00 | 0 | -2,72 | 5,01 |
| 3 | Полоса | 36,00 | 12,00 | 972,00 | 0 | 4,07 | -6,99 |
| S | Все сечение | 73,37 |
Продолжение табл. 3.7
| Наименование элемента | "Переносные" моменты инерции, см4 | Моменты инерции относительно
центральных осей 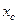 и и 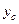 , см4 , см4
| ||||
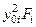
|  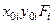
| 
| 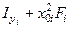
| 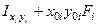
| ||
| Уголок | 515,39 | 1298,12 | -817,95 | 1346,28 | 563,55 | -789,76 |
| Швеллер | 197,54 | 670,17 | -363,85 | 2780,17 | 348,54 | -363,85 |
| Полоса | 596,34 | 1758,96 | -1024,17 | 1770,96 | 1568,34 | -1024,17 |
| Все сечение | 5897,41 | 2480,43 | -2177,78 |
После округления вычисленных значений моментов инерции до трех значащих цифр, окончательно, получим
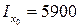 см4;
см4;  см4;
см4;  см4.
см4.
Определяем положение главных центральных осей инерции u и v
Угол наклона главных центральных осей u и v к центральным осям 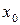 и
и  соответственно определяем из следующей формулы:
соответственно определяем из следующей формулы:
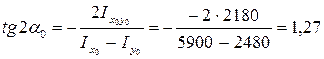 .
.
Отсюда находим, что 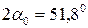 и
и  .
.
Откладываем положительное значение угла 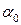 от оси
от оси 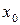 против хода часовой стрелки и проводим главные центральные оси u и v (см. рис. 3.10).
против хода часовой стрелки и проводим главные центральные оси u и v (см. рис. 3.10).
Ось, относительно которой момент инерции максимален, составляет меньший угол с той из центральных осей 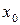 или
или  , относительно которой осевой момент больше. Поскольку
, относительно которой осевой момент больше. Поскольку 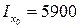 см4 больше, чем
см4 больше, чем  см4, ось u является осью относительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.
см4, ось u является осью относительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.
|
|
|
Вычисляем значения главных центральных моментов инерции 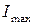 и
и 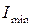 для заданного поперечного сечения
для заданного поперечного сечения
Значения главных центральных моментов инерции всей фигуры определяются по формуле
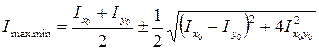 .
.
Тогда
 см4;
см4;
 см4;
см4;  см4.
см4.
Контролем правильности последних вычислений может служить следующее условие:
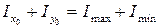 .
.
Имеем
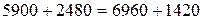 ,
, 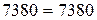 .
.
Условие задачи для самостоятельного решения по теме "геометрические характеристики плоских сечений"
Для заданного поперечного сечения стержня (рис. 3.9), состоящего из двух прокатных профилей и полосы, требуется найти положение центра тяжести сечения, направление главных центральных осей инерции u и v, а также вычислить главные центральные моменты инерции  и
и  . Данные взять из табл. 3.5 и табл. и из сортамента двутавров, уголков и швеллеров.
. Данные взять из табл. 3.5 и табл. и из сортамента двутавров, уголков и швеллеров.
Вопросы для самоконтроля представить вместе с развернутыми конспектами по данной теме и решение задач на эл почту bervengas@inbox.ru
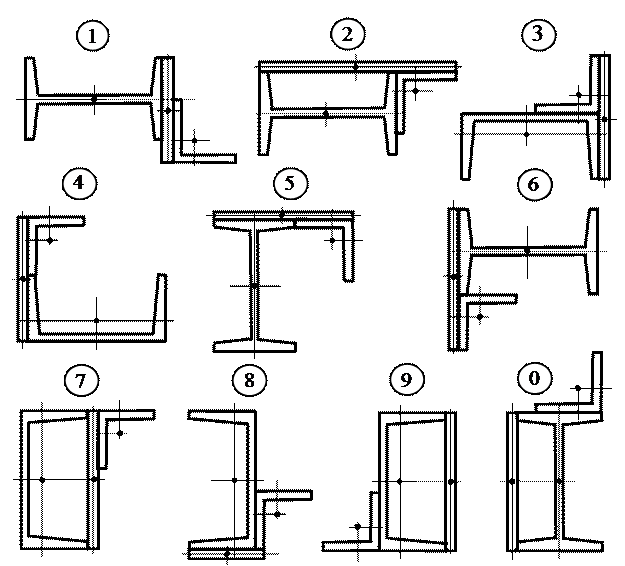
|
Таблица 3.5
| Номер схемы (рис. 3.9) | Номер швеллера | Номер двутавра | Размеры уголка | Толщина листа, мм |
| 1 | 24 | 12 | 100×100×8 | 12 |
| 2 | 22 | 14 | 100×100×10 | 12 |
| 3 | 20 | 16 | 100×100×12 | 12 |
| 4 | 18 | 18 | 100×100×8 | 14 |
| 5 | 16 | 20 | 100×100×10 | 14 |
| 6 | 14 | 22 | 100×100×12 | 14 |
| 7 | 12 | 24 | 100×100×8 | 16 |
| 8 | 24 | 22 | 100×100×10 | 16 |
| 9 | 22 | 20 | 100×100×12 | 16 |
| 0 | 20 | 18 | 100×100×8 | 10 |
Решение задач по сопромату рекомендуется производить по правилам:
Перед решением задачи по сопромату необходимо переписать полностью ее условие с числовыми данными, составить эскиз в масштабе и указать на нем в числах все величины, необходимые для дальнейшего расчета,
Решение задач по сопромату дополняйте краткими пояснениями и чертежами, на которых визуализированы входящие в расчет величины,
Перед использованием формулы для определения напряженно-деформированного состояния необходимо изучить соответствующую тему лекций по сопромату, чтобы понять физический смысл всех величин, входящих в нее,
При подстановке в используемую формулу величин силы, момента или длины необходимо перевести их в одну систему единиц,
При решении задач по сопромату точность расчетов не должна превышать трех значащих цифр (результат решения задачи не может быть точнее заложенных в расчетные формулы предпосылок),
Заканчивать расчеты нужно анализом результатов - преподавали по сопромату таким образом проверяют ваши работы. Анализ результатов решения поможет избежать нелепых ошибок и оперативно их устранить.
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

Приложим теперь к стержню растягивающую силу 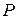 (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение
(рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение  , а частица L – в положение
, а частица L – в положение 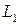 . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил 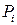 (рис. 1.2, а) на две части плоскостью, перпендикулярной к его оси z.
(рис. 1.2, а) на две части плоскостью, перпендикулярной к его оси z.
Отбросим одну из частей стержня и рассмотрим оставшуюся часть.
Теперь в каждой точке поперечного сечения возникают силы упругости, которые называются внутренними силами (рис 1.2 б).
 2020-05-25
2020-05-25 330
330








