2020-05-21
172
Пусть
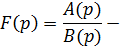
дробно-рациональная функция, у которой степень многочлена, стоящего в числителе меньше степени многочлена, стоящего в знаменателе.
Обозначим 
полюсы 
их кратности.
Тогда
В частности, если все полюсы простые
Доказательство. Следует из второй теоремы разложения.
Квант 11.01.04.04. Оригинал дробно-рациональной функции с действительными коэффициентами (Т).
Пусть
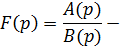
дробно-рациональная функция, у которой степень многочлена, стоящего в числителе меньше степени многочлена, стоящего в знаменателе и многочлены 
и 
имеют действительные коэффициенты.
Обозначим 
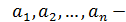полюсы 
, лежащие на действительной оси, 
полюсы , лежащие в верхней полуплоскости.
Тогда
Доказательство. Пусть 
корень многочлена 
Т.к. многочлен 
имеет действительные коэффициенты, то
т.е. 
тоже корень многочлена 
. Корни многочлена с действительными коэффициентами попарно комплексно сопряжены. Значит каждому полюсу функции , лежащему в верхней полуплоскости соответствует полюс, лежащий в нижней полуплоскости (симметрично относительно действительной оси). Вычеты в комплексно сопряженных полюсах также будут комплексно сопряженными числами, а сумма комплексно сопряженных чисел равна удвоенной действительной части одного из них.
Пример.
С помощью первой теоремы разложения мы получили
Получим этот результат с помощью второй теоремы разложения.
Точка 
является существенно особой и для нахождения вычета в ней нужно найти коэффициент 
разложения Лорана.
Параграф 11.01.05. Предельные соотношения. Интеграл Дюамеля.
Квант 11.01.05.01. Связь начального значения оригинала и конечного значения изображения (Т).
Пусть 
и 
являются оригиналами.
Если существует
то
Доказательство.
Поскольку предел изображения при 
равен нулю (квант 11.01.02.02), то
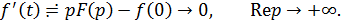
Квант 11.01.05.02. Связь конечного значения оригинала и начального значения изображения (Т).
Пусть является оригиналом.
Если существует
то
Доказательство.
Переходя в этом равенстве к пределу при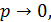 
получим
Пример.
