Квант 11.01.05.03. Интеграл Дюамеля (Т)

    Пусть  являются оригиналами.

 

Если

  то

Доказательство.  

Пользуясь теоремами о дифференцировании оригинала, о свертке и коммутативностью свертки, получаем

Меняя ролями функции  и , получаем

Параграф 11.01.06. Операционный метод решения линейных дифференциальных уравнений и систем.

 

 

Квант 11.01.06.01. Операционный метод решения задачи Коши для линейного неоднородного дифференциального уравнения с действительными коэффициентами.

    Рассмотрим задачу Коши для ЛНДУ го порядка с постоянными действительными коэффициентами

и произвольными начальными условиями

Будем считать, что правая часть , искомая функция  и ее производные до го порядка включительно являются оригиналами.

 

Применим преобразование Лапласа к левой и правой частям дифференциального уравнения.

Вместо дифференциального уравнения получим алгебраическое уравнение для изображений (операторное уравнение)

Решая это уравнение относительно 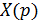, получим

  Тогда решением задачи Коши будет оригинал

Пример.

Решить задачу Коши

Решение.

1) Применяем преобразование Лапласа.

Получим линейное алгебраическое уравнение относительно

2) Решаем это уравнение.

3) Находим оригинал функции , который будет решением задачи Коши. Оригинал найдем, пользуясь таблицей и свойствами преобразования Лапласа.

Поскольку

то дифференцируя изображение, получим

Теперь делим изображение на 2  и пользуемся свойством интегрирования оригинала.

 

 

Таким образом, решением задачи Коши будет функция