2020-05-21
1089
Рассмотрим задачу Коши для ЛНДУ 
го порядка с постоянными действительными коэффициентами
и нулевыми начальными условиями
Будем считать, что правая часть 
, искомая функция 
и ее производные до го порядка включительно являются оригиналами.
Если известно решение 
соответствующей задачи Коши с правой частью равной единице (функции Хевисайда):
то решение исходной задачи Коши записывается в виде свертки
или
Доказательство.
Операторные уравнения исходной задачи Коши с правой частью 
и задачи Коши с правой частью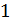 
будут иметь вид
и
соответственно. Имеем
Применяя интеграл Дюамеля (квант 11.01.05.03), получим доказываемые формулы.
Пример.
Решить задачу Коши
Найдем решение задачи Коши с единицей в правой части уравнения
Применим преобразование Лапласа, получим операторное уравнение
Его решением является функция
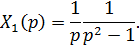
Ее оригиналом будет
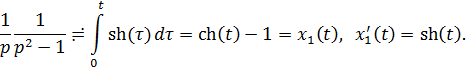
Решение исходной задачи Коши получаем с помощью интеграла Дюамеля
или
Квант 11.01.06.03. Операционный метод решения задачи Коши для системы линейных дифференциальных уравнений.
Рассмотрим задачу Коши для системы 
ЛНДУ 2 
го порядка с постоянными действительными коэффициентами
и произвольными начальными условиями
Применим преобразование Лапласа
Вместо системы дифференциальных уравнений с начальными условиями получим операторную систему линейных алгебраических уравнений
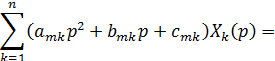
Решив эту систему, найдем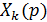 
, 
Тогда решением задачи Коши будут оригиналы
Пример.
Решить систему дифференциальных уравнений с заданными начальными условиями. Сделать проверку.
Решение.
Применяем преобразование Лапласа.
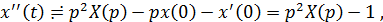
Решаем полученную линейную систему уравнений.
Разлагаем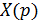 
на простейшие дроби
Оригиналы найдем по таблице
Проверка:
