Разделим весь рассматриваемый интервал времени Т на N одинаковых интервалов, длительностью  . Порядковый номер интервалов обозначим через i. Вследствие ординарности потоков заявок, в течение каждого i - го интервала времени поступает целое число заявок
. Порядковый номер интервалов обозначим через i. Вследствие ординарности потоков заявок, в течение каждого i - го интервала времени поступает целое число заявок  (i = 0,1,2...). Число заявок, поступающих в течение времени
(i = 0,1,2...). Число заявок, поступающих в течение времени  , является дискретной случайной величиной с математическим ожиданием
, является дискретной случайной величиной с математическим ожиданием 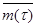 , вторым начальным моментом
, вторым начальным моментом  и дисперсией
и дисперсией  .
.
Допустим, что в течение каждого i - го интервала времени в СМО находится  заявок, ожидающих в очереди. Длина очереди также является дискретной случайной величиной с математическим ожиданием
заявок, ожидающих в очереди. Длина очереди также является дискретной случайной величиной с математическим ожиданием  .
.
Обозначим через  элемент последовательности случайных чисел, сдвинутый влево относительно
элемент последовательности случайных чисел, сдвинутый влево относительно  на j промежутков времени
на j промежутков времени  . Вторые взаимные начальные моменты последовательностей
. Вторые взаимные начальные моменты последовательностей 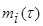 и
и  , как математические ожидания произведений их соответствующих элементов.
, как математические ожидания произведений их соответствующих элементов.

Вторые взаимные центральные моменты указанных последовательностей, называемые корреляционными моментами или ковариацией, определяются как математические ожидания произведений центрированных значений их элементов.
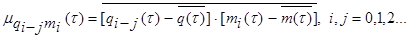
Между указанными моментами существует соотношение:

Билет №7
 2020-05-25
2020-05-25 197
197








