Свойства сходящихся последовательностей

1. Если последовательность сходится, то только к одному пределу.

2. Если последовательность сходится, то она ограничена.

3. Если последовательность монотонна и ограничена, то она сходится.

Если , то последовательность у_n= qⁿ расходится.

 

Теоремы о пределах последовательностей.

1.

2. Если

3. Если , то

4. Для любого натурального показателя m и любого коэффициента k справедливо соотношение:

5. Предел суммы равен сумме пределов:

6. Предел произведения равен произведению пределов:

7. Предел частного равен частному пределов: , где с≠0.

8. Постоянный множитель можно выносить за знак предела:

Нахождение пределов последовательности:

Найти предел последовательности:

а) х_n = б) х_n = в)

Решение: а) применив правило «предел произведения», получим:

б) применим правило «предел суммы» и получим:

в) в подобных случаях применяют искусственный прием: делят числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n. В данном примере разделим числитель и знаменатель дроби почленно на n². Имеем: 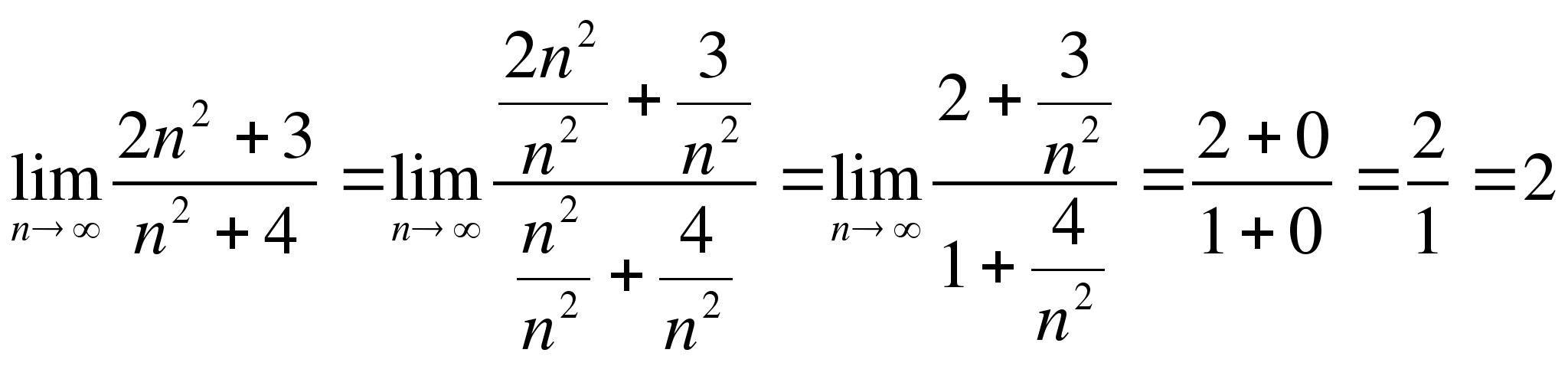(здесь мы применили правило «предел дроби»).

Пределы функций. Нахождение пределов функции в точке и на бесконечности.

Теория пределов позволяет определить характер поведения функции у = f(x) при заданном изменении аргумента.

Пусть функция f(х) определена в некоторой окрестности точки х =х₀, за исключением, быть может, самой точки х₀.

Число А называется пределом функции f(х) в точке х₀, если для любого числа >0 найдется такое положительное число , что для любого х х₀, удовлетворяющего неравенству | х - хо | < , выполняется соотношение | f(x) - А | <

То, что функция f(x) в точке х₀ имеет предел, равный А, обозначают следующим образом:

Геометрически существование данного предела означает, что каково бы ни было >0, найдется такое число , что для всех х, заключенных между х₀ + , и х₀ - (кроме, быть может, самой точки х_с), график функции у = f(x) лежит в полосе, ограниченной прямыми у = А + и у = А- (рис.1)

Рисунок 1

Таким образом, понятие предела функции дает возможность ответить на вопрос, к чему стремятся значения функции, когда значения аргумента стремятся к х₀

Число А называют пределом функции f(x) при х, стремящимся к х₀, если разность f(x) - А по абсолютной величине есть величина бесконечно малая.