2020-05-21
1082
Задержка – один из критериев обслуживания СМО, время проведенное заявкой в ожидании обслуживания.
Пусть:
Di – задержка в очереди требования i;
Wi=Di+Si – время нахождения в системе требования i.
Тогда показатели (если существуют)
(с вероятностью 1) – установившаяся средняя задержка требования в очереди;
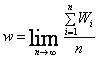(с вероятностью 1) – установившееся среднее время нахождения требования в СМО (waiting).
Пусть:
Q(t) – число требований в очереди в момент времени t;
L(t) – число требований в системе в момент времени t (Q(t) плюс число требований, которые находятся на обслуживании в момент времени t.
Тогда показатели (если существуют)
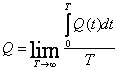(с вероятностью 1) – установившееся среднее по времени число требований в очереди;
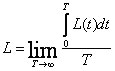(с вероятностью 1) – установившееся среднее по времени число требований в системе.
Заметим, что ρ<1 – обязательное условие существования d, w, Q и L в системе массового обслуживания.
Если вспомнить, что ρ= λ/(N μ), то видно, что если интенсивность поступления заявок больше, чем N μ, то ρ>1 и естественно, что система не сможет справиться с таким потоком заявок, а следовательно, нельзя говорить о величинах d, w, Q и L.
|
|
|
К наиболее общим и нужным результатам для систем массового обслуживания относятся уравнения сохранения
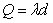
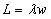
Следует обратить внимание, что упомянутые выше критерии оценки работы системы могут быть аналитически вычислены для систем массового обслуживания M/M/N (N >1), т. е. систем с Марковскими потоками заявок и обслуживания. Для М/G/ l при любом распределении G и для некоторых других систем. Вообще распределение времени между поступлениями, распределение времени обслуживания или обеих этих величин должно быть экспоненциальным (или разновидностью экспоненциального распределения Эрланга k-го порядка), чтобы аналитическое решение стало возможным.
Кроме этого можно также говорить о таких характеристиках, как:
· абсолютная пропускная способность системы – А=Робсл*λ;
· относительная пропускная способность системы –
Еще один интересный (и наглядный) пример аналитического решения – вычисление установившейся средней задержки в очереди для системы массового обслуживания M/G/ 1 по формуле:
.
В России эта формула известна как формула Поллачека – Хинчина, за рубежом эта формула связывается с именем Росса (Ross).
Таким образом, если E(S) имеет большее значение, тогда перегрузка (в данном случае измеряемая как d) будет большей; чего и следовало ожидать. По формуле можно обнаружить и менее очевидный факт: перегрузка также увеличивается, когда изменчивость распределения времени обслуживания возрастает, даже если среднее время обслуживания остается прежним. Интуитивно это можно объяснить так: дисперсия случайной величины времени обслуживания может принять большое значение (поскольку она должна быть положительной), т. е. единственное устройство обслуживания будет занято длительное время, что приведет к увеличению очереди.
|
|
|
Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования. В большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.
Случайный характер потока заявок (требований), а также, в общем случае, и длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс. По характеру случайного процесса, происходящего в системе массового обслуживания (СМО), различают системы марковские и немарковские. В марковских системах входящий поток требований и выходящий поток обслуженных требований (заявок) являются пуассоновскими. Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют марковскую схему. В случае немарковских процессов задачи исследования систем массового обслуживания значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.
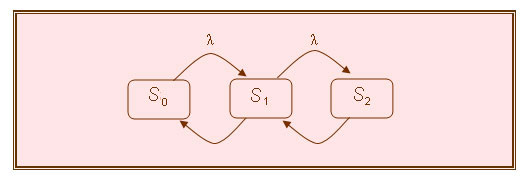
Рассмотрим непрерывные марковские цепи, которые характеризуют процессы гибели и размножения. Количество событий соответствует количеству каналов. S 0 – событие «все свободны, нет занятых каналов»; S 1 – один канал занят, и т. д. Таким образом имеем процесс, в котором каждому событию соответствует целое число, которое характеризует количество занятых каналов. Событие заключается в том, что количество занятых каналов может уменьшиться на 1, или увеличиться на 1.
