2020-05-25
745
Изучим вопрос: В каких пределах могут меняться значения коэффициентов целевой функци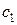и 
и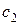 
, так чтобы оптимальный план оставался неизменным, для рассматриваемого примера 
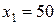и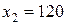 
.
Допустим, значение 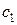изменяется, а значение 
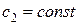, т.е. фиксировано. При этом вектор 
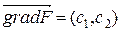также изменит направление и величину. В каких пределах может меняться значение , 
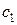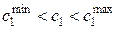, чтобы оптимальный план 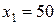и 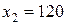оставался неизменным. Изменение значения 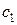приведет к такому расположению линейной формы (целевой функции 
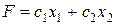), когда линейная форма станет параллельной поочередно сначала одной из прямых, ограничивающих область допустимых решений в оптимальном плане, потом другой, т.е. значение 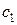изменим таким образом, чтобы линейная форма поочередно стала параллельной двум прямым, на пересечении которых находится оптимальный план. Из условия параллельности прямых, пропорциональности коэффициентов, имеем:
║ 
.
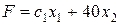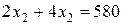Отсюда получим: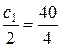 
.
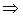
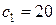Проверяем параллельность линейной формы ко второй прямой, образующей оптимальное решение:
║ 
.
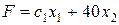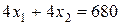Отсюда получим: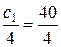 
.
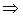
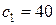Таким образом, значение 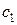меняется в пределах: 
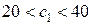, а в задании 
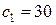. При этом значение целевой функции в оптимальной точке 
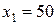и 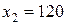меняется в пределах: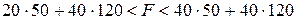 
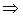
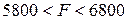, а в задании максимальное значение целевой функции 
.
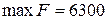Аналогичные результаты можно получить при изменении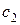 
с учетом 
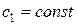. В каких пределах может меняться значение , 
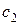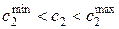, чтобы оптимальный план 
и 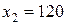оставался неизменным. Значение 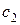изменим таким образом, чтобы линейная форма поочередно стала параллельной двум прямым, на пересечении этих прямых находится оптимальный план. Из условия параллельности прямых, пропорциональности коэффициентов, имеем:
║ 
.
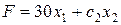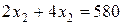Отсюда получим: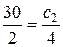 
.
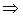
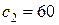Проверяем параллельность линейной формы ко второй прямой, образующей оптимальное решение:
║ .
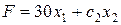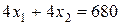Отсюда получим: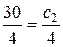 
.
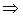
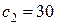Таким образом, значение 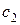меняется в пределах: 
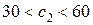, а в задании 
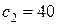. При этом значение целевой функции в оптимальной точке 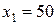и 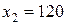меняется в пределах: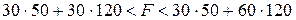 
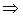
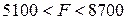, а в задании максимальное значение целевой функции .
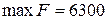Выводы:
1) В результате решения прямой задачи получен следующий оптимальный план выпуска продукции: 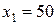, 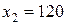(ед.). При этом максимальная прибыль равна 6300.
2) В результате решения двойственной задачи получены оптимальные значения оценок ресурсов: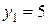 
, 
, 
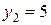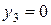. При этом суммарная оценка всех ресурсов (минимальное значение), используемых в производстве равна 6300.
3) Максимальная прибыль равна минимальной оценке всех ресурсов, т.е.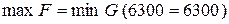 
4) Положительную оценку имеют лишь те ресурсы, которые полностью израсходованы. Оценка третьего ресурса равна нулю (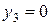
), т.к. он оказался полностью не израсходованным (
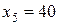). Первое и второе ограничения прямой задачи выполняются как равно (=), третье ограничение выполняется как «неравно» (<).
