Рассмотрим решение задачи ЛП с помощью модуля «Поиск Решения» в Excel, предназначенного для решения задач оптимизации. Алгоритм решения прямой и двойственной задач представим в виде электронной таблицы.
Запустим программу Excel и для рассматриваемой задачи составим электронную таблицу (рис.1). В ячейках B3 и C3 запишем входные значения плана 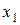 и
и 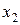 . В результате решения задачи в этих ячейках мы получим оптимальные значения плана. В ячейках B5 и C5 запишем значения коэффициентов целевой функции. В ячейке A7 разместим значение целевой функции в виде «=суммпроизв(B3:C3; B5:C5)».
. В результате решения задачи в этих ячейках мы получим оптимальные значения плана. В ячейках B5 и C5 запишем значения коэффициентов целевой функции. В ячейке A7 разместим значение целевой функции в виде «=суммпроизв(B3:C3; B5:C5)».
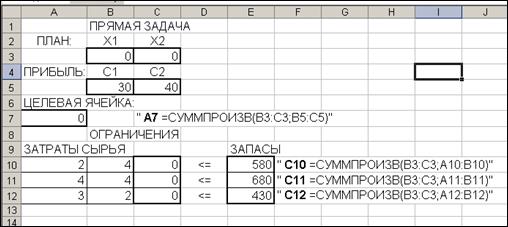
Рис.1
Левую часть системы ограничений по сырьевым ресурсам запишем в ячейки C10 – C12 в виде: в ячейку C10 «=суммпроизв(B3:C3; A10:B10)», C11 «=суммпроизв(B3:C3; A11:B11)», C12 «=суммпроизв(B3:C3; A12:B12)». Запасы ресурсов: 580, 680, 430 – значения 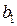 ,
, 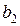 ,
, 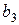 , запишем в ячейки E10:E12. В надстройках EXCEL найдем Поиск решения и запустим его. В появившемся диалоговом окне (рис.2) занесем необходимые данные:
, запишем в ячейки E10:E12. В надстройках EXCEL найдем Поиск решения и запустим его. В появившемся диалоговом окне (рис.2) занесем необходимые данные:
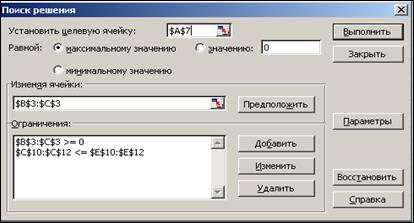
Рис.2.
адрес ячейки целевой функции $A$7; направление оптимизации – максимум; адреса изменяемых ячеек $B$3:$C$3.
Ограничения вводятся в окне Добавление ограничения (рис.3) которое активизируется кнопкой Добавить окна Поиск решения.
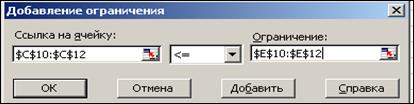
Рис.3.
Левая часть системы ограничений по сырьевым ресурсам не превышает правой части, т.е. затраты ресурсов на производство не превышают запасов. В окне Добавление ограничения эти условия представляются в виде «$C$10:$C$12<=$E$10:$E$12», как указано на рис.3.
Следует добавить условие, что план должен быть не отрицательным «$B$3:$C$3 >=0».
В окне Параметры поиска решения (рис.4) вызванном командой
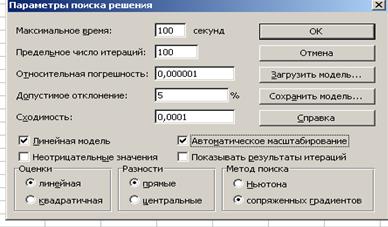
Рис.4.
Параметры окна Поиск решения (рис.2) установим флажки: Автоматическое масштабирование, сопряженных градиентов (выбранный численный метод решения задачи). Следует установить флажок Линейная модель. Далее, щелкнув левой кнопкой мыши по ОК, возвратимся в окно Поиск решения. В этом окне, щелкнув левой кнопки мыши по команде Выполнить, получим оптимальное решение задачи (рис.5).
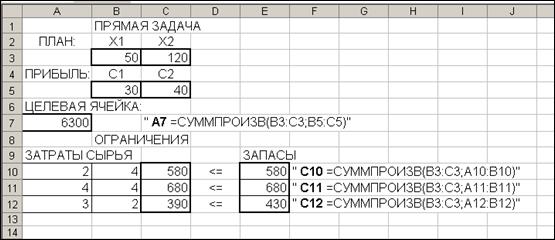
Рис.5.
Оптимальное решение задачи (рис.5) располагается в изменяемых ячейках B3 и C3, в ячейке B3 находится значение 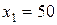 , а в ячейке C3 находится значение
, а в ячейке C3 находится значение 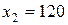 . Максимальное значение целевой функции располагается в ячейке A7:
. Максимальное значение целевой функции располагается в ячейке A7: 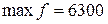 . Нетрудно убедиться, что все ограничения задачи выполняются.
. Нетрудно убедиться, что все ограничения задачи выполняются.
Далее рассмотрим решение двойственной задачи (рис.6).
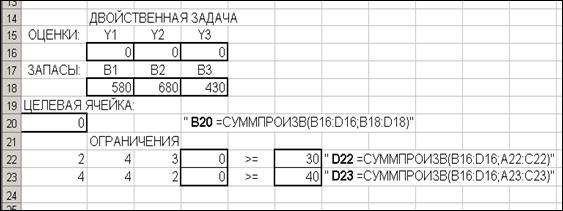
Рис.6
В электронную таблицу, составленную для решения прямой задачи (рис.1), добавим алгоритм решения двойственной. В ячейках B16 – D16 запишем входные значения оценок сырья 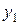 ,
, 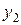 ,
, 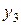 . В результате решения двойственной задачи в этих ячейках мы получим оптимальные значения оценок. В ячейках B18 – D18 запишем 580, 680, 430 – значения
. В результате решения двойственной задачи в этих ячейках мы получим оптимальные значения оценок. В ячейках B18 – D18 запишем 580, 680, 430 – значения 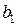 ,
, 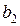 ,
, 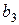 , которые являются коэффициентами целевой функции двойственной задачи. В ячейке A20 разместим значение целевой функции двойственной задачи в виде «=суммпроизв(B16:D16; B18:D18)». Левую часть системы ограничений двойственной задачи, которая определяет суммарную оценку всех видов сырья для производства единицы продукции каждого вида, запишем в ячейки D22 – D23 в виде: в ячейку D22 «=суммпроизв (B16:D16; A22:C22)», в ячейку D23 «=суммпроизв(B16:D16; A23:C23)». В ячейки F22:F23 вводятся 30, 40 – значения
, которые являются коэффициентами целевой функции двойственной задачи. В ячейке A20 разместим значение целевой функции двойственной задачи в виде «=суммпроизв(B16:D16; B18:D18)». Левую часть системы ограничений двойственной задачи, которая определяет суммарную оценку всех видов сырья для производства единицы продукции каждого вида, запишем в ячейки D22 – D23 в виде: в ячейку D22 «=суммпроизв (B16:D16; A22:C22)», в ячейку D23 «=суммпроизв(B16:D16; A23:C23)». В ячейки F22:F23 вводятся 30, 40 – значения 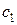 и
и 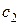 , которые являются правой частью системы ограничений двойственной задачи.
, которые являются правой частью системы ограничений двойственной задачи.
Для получения оптимального решения двойственной задачи запустим надстройку Поиск решения. В появившемся диалоговом окне занесем необходимые данные аналогично как при решении прямой задачи: адрес ячейки целевой функции – $A$20; направление оптимизации – минимум; адреса изменяемых ячеек – $B$16:$D$16. В окне Добавление ограничения введем ограничения двойственной задачи в виде «$D$22:$D$23>=$F$22:$F$23». Следует также добавить условие, что оценки 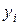 должны быть не отрицательными «$B$16: $D$16>=0». В результате выполнения процедуры Поиска решения получим оптимальное решение двойственной задачи (рис.7).
должны быть не отрицательными «$B$16: $D$16>=0». В результате выполнения процедуры Поиска решения получим оптимальное решение двойственной задачи (рис.7).
Отметим ряд важных свойств между решениями прямой задачи и двойственной, которые приведены на рис.5 и на рис.7.
1) Максимальная прибыль в прямой задаче равна 6300 ед. (на рис.5 ячейка A7). Минимальная суммарная оценка всех ресурсов в двойственной задаче также равна 6300 ед. (на рис.7 ячейка A20). Таким образом, экстремальные значения целевых функций прямой и двойственной задач равны:
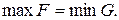

Рис.7
2) Положительную оценку имеют лишь те виды сырья, которые полностью используются в оптимальном плане. Оценки первого и второго вида сырья положительны: 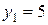 и
и 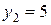 (на рис.7 ячейки B16 и C16). В прямой задаче первый и второй вид сырья полностью израсходованы (на рис.5 значения в ячейках C10=E10 и C11=E11). Оценка третьего вида сырья равна нулю:
(на рис.7 ячейки B16 и C16). В прямой задаче первый и второй вид сырья полностью израсходованы (на рис.5 значения в ячейках C10=E10 и C11=E11). Оценка третьего вида сырья равна нулю: 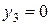 (на рис.7 ячейка D16). В прямой задаче третий вид сырья полностью не израсходован (на рис.5 значение ячейки C12 < E12). Третий вид сырья остался в излишках на 40 ед. Можно отметить и другие взаимосвязи между прямой задачей и двойственной.
(на рис.7 ячейка D16). В прямой задаче третий вид сырья полностью не израсходован (на рис.5 значение ячейки C12 < E12). Третий вид сырья остался в излишках на 40 ед. Можно отметить и другие взаимосвязи между прямой задачей и двойственной.
На рис.8 приводятся результаты вычисления интервалов устойчивости двойственных оценок на изменение количества сырья и устойчивости оптимального плана на изменение стоимости продукции с помощью процедуры Поиск решения.
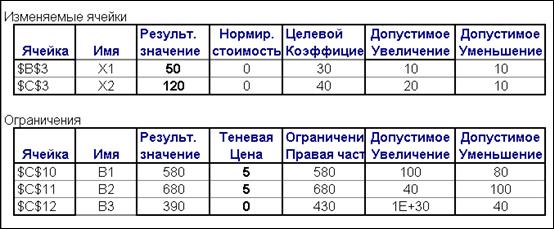
Рис.8
По результатам устойчивости на рис.8, полученным с помощью надстройки Excel, можно отметить:
1) оптимальное решение прямой задачи ЛП 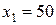 и
и 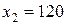 не поменяется при изменении коэффициентов целевой функции в переделах:
не поменяется при изменении коэффициентов целевой функции в переделах: 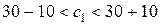 и
и 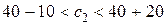 ;
;
2) оптимальное решение двойственной задачи ЛП (теневая цена) 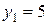 ,
, 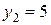 ,
, 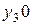 не поменяется при изменении запасов сырья в пределах:
не поменяется при изменении запасов сырья в пределах: 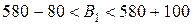 ,
, 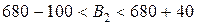 ,
, 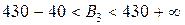 ;
;
 2020-05-25
2020-05-25 159
159







