РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Во многих научных и инженерных задачах возникает необходимость решения уравнений вида
f(x)=0 (1)
Всякое число, обращающее функцию f(x) в нуль, называется корнем уравнения (1). Нелинейные уравнения подразделяются на алгебраические и трансцендентные.
Уравнение (1) называется алгебраическим, если функция f(x) является алгебраической или трансцендентным, если функция f(x) не является алгебраической.
Численное решение уравнения (1) обычно проводят в два этапа. На первом этапе необходимо отделить корни уравнения, т.е. найти такие интервалы изменения переменной х, где расположен только один корень (интервалы изоляции корня). На втором этапе проводят уточнение отделенных корней, т.е. находят корни с заданной точностью.
Отделение корней
Рассмотрим графический способ отделения корней уравнения (1), который используется, когда отсутствует информация о расположении корней. В интересующей нас области изменения неизвестного (интервал отделения) xÎ[x0, xn] вычислим ряд значений левой части уравнения (1) и результаты поместим в табл. 1, по которой можно построить график (рис. 1), из которого следует, что на данном интервале уравнение имеет 3 корня.
| Таблица 1 | |
| x | f (х) |
| x0 | f0 |
| x1 | f1 |
| … | … |
| xn | fn |
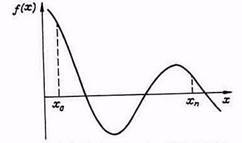
Рисунок 1. График левой части уравнения
Шаг изменения аргумента х при вычислении табл. 1 выбирается так, чтобы он был меньше расстояния между корнями. Только в этом случае удается отделить все корни.
Автоматизация нахождения интервалов изоляции основана на свойстве интервалов изоляции, заключающемся в различии знаков функции f (х) на их границах. Пример процедуры Roots, реализующей данный подход, приведен ниже. Параметры, передаваемые в процедуру: f -имя функции; а и б- границы интервала отделения ;N- количество подинтервалов. Ниже приведен пример отделения корней для уравнения 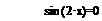 на отрезке [-0,1;6,5].
на отрезке [-0,1;6,5].
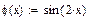
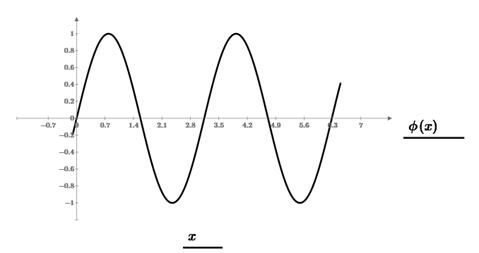
Из графика видно, что на данном интервале уравнение имеет 5 корней.
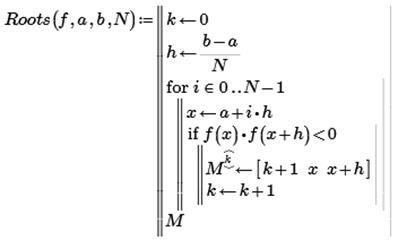
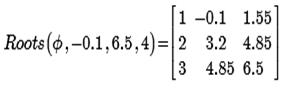
При четырех подинтервалах (крупном шаге) удалось отделить только 3 из 5 корней.
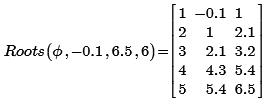
При шести подинтервалах (мелком шаге) удалось отделить все 5 корней.
Методы уточнения корней
Метод дихотомии
Считаем, что отделение корней уравнения (1) проведено и на интервале изоляции [а, b] расположен один корень, который необходимо уточнить с погрешностью e (рис. 2).
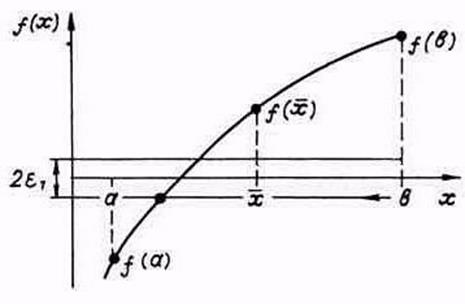
Рисунок 2. Метод дихотомии
Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b]: 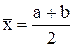 и вычисляем функцию
и вычисляем функцию 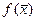 . Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. На рис. 3 это будет отрезок [а,
. Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. На рис. 3 это будет отрезок [а, 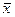 ], т.е. для очередного шага уточнения точку b перемещаем в точку
], т.е. для очередного шага уточнения точку b перемещаем в точку 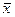 и продолжаем процесс деления как с первоначальным отрезком [а, b].
и продолжаем процесс деления как с первоначальным отрезком [а, b].
Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а, b] не станет меньше заданной погрешности e:
|xn-xn-1|<e
или когда значения функции f(x) (невязки) не станут достаточно малы
|f(xn)|<e1
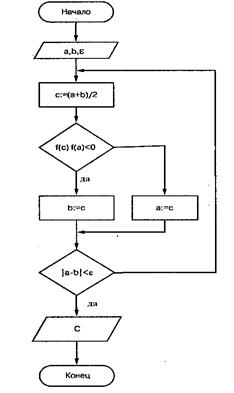
Рисунок 3. Алгоритм метода дихотомии
 2020-05-21
2020-05-21 154
154







