Интегрирование по частям

Таблица основных интегралов

1.             

2.

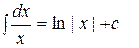
3.  

4.                              

5.                     

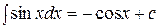
6.                     

7.  

8.

9.                 

10.                   

11.  

12.

Интегрирование и дифференцирование – взаимно обратные операции.

Свойства неопределенного интеграла

    Если y = f (x), y = F (x), y = g (x) – некоторые функции, то:

1)

2)

3)

Некоторые методы интегрирования

Непосредственное интегрирование

    Метод непосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путем преобразований и применения свойств неопределённого интеграла.

Примеры

1) Вычислить: .

Решение:

2) Вычислить: .

Решение:

3) Вычислить: .

Решение:

Интегрирование методом замены переменной (метод подстановки)

    Часто бывает так, что предлагаемый для вычисления интеграл не содержится в таблице интегралов и не сводится к табличным интегралам. Тогда применяются другие методы интегрирования, одним из которых является метод замены переменной.

    Пусть имеет место неопределенный интеграл , где подынтегральная функция непрерывна. Применив подстановку  и вычислив дифференциал 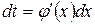, получим  – формулу замены переменной в неопределённом интеграле.

    Сложность применения метода замены переменной заключается в том, что метод не даёт инструкции о том, какую замену требуется применить в том или другом случае для того, чтобы свести данный интеграл к табличному.

Пример

         Вычислить интеграл .

Решение: Обозначим . Дифференцируя обе части этого выражения, найдём, чему равно dx, т.е. . Тогда

.

Пример

    Вычислить интеграл .

Решение:

Выделим в знаменателе подынтегрального выражения  полный квадрат, получим

, тогда

.

Пример

         Вычислить интеграл .

Решение: = =

Интегрирование по частям

Формула интегрирования по частям имеет вид:

,

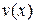 где  и  – дифференцируемые функции.

В ряде случаев она позволяет свести предлагаемый для вычисления интеграл к более простому, возможно, к табличному. При этом необходимо знать, что интегралы, вычисляемые данным методом, разделяются на две группы.

I группа

Если имеем интегралы вида: , , , , то за функцию принимаем многочлен , за  – оставшееся выражение.

II группа

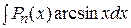
Если имеем интегралы вида: , , , , то , а за функцию принимаем оставшуюся функцию 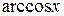, , , , . В частном случае , тогда .

Пример

Вычислить интеграл .

Решение: Так как данный интеграл относится к группе I, то имеем в предлагаемом интеграле ; тогда , , . Из всей совокупности полученных функций  выберем какую-нибудь одну; пусть, например, С = 0. Тогда

.

Пример

Вычислить интеграл .

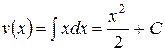Решение: Так как данный интеграл относится к группе II, то , тогда , , . Из всей совокупности полученных функций  выберем какую-нибудь одну; пусть, например, С = 0. Тогда

.