2020-06-12
563
Уравнение одновального ТРД с неизменной геометрией проточной части. Для упрощения исследования переходных процессов ТРД обычно пренебрегают запаздыванием, связанным с изменением топливного режима и с наличием некоторого объема между компрессором и турбиной. При этом имеет место известное уравнение механики
(2.1)
где: ω – угловая частота вращения ротора, равная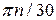 
, 
– крутящий момент на турбине, 
-крутящий момент поглощаемый компрессором, J- момент инерции ротора.
 |
n 
Рис. 2.2
Установившийся режим работы определяется равенством крутящих моментов ротора и турбины 
. Здесь и далее параметры, соответствующие установившимся (потребным) режимам работы, будем помечать индексом «з». Пусть этому режиму соответствуют обороты 
, количество топлива 
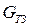и давление перед компрессором 
. При изменении положения РУД или режима полета (снижение, набор высоты) баланс моментов нарушается (появляется избыточный момент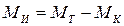 
) и наступает переходный режим, описываемый уравнением (2.1). Поскольку для данного типа двигателя имеется одно управляющее воздействие и одна управляемая величина (рис.2.2), то можно предположить, что избыточный момент является функцией расхода топлива, количества оборотов и давления перед компрессором 
. Разложим эту функцию в ряд Тейлора в окрестности равновесного состояния (
) с удержанием первых производных
(2.2)
С учетом того, что при равновесном режиме 
, после подстановки (2.2) в уравнение (2.1) получим
(2.3)
Обычно вместо отклонений для получения безразмерных параметров в
теории автоматического управления вводят так называемые базовые координаты, представляющие собой отношение отклонений к некоторому номинальному или базовому уровню
Δ 
(2.4)
Подставляя (2.4) в (2.3), опуская индекс <<б>> для краткости записи и
проводя преобразования, окончательно получим
(2.5)
В отношении (2.5)
(2.6)
Если внешние возмущения отсутствуют 
,то уравнение
динамики ГТД (2.5) примет вид
(2.7)
Коэффициент 
называется постоянной времени двигателя, коэффициенты 
, 
- коэффициенты усиления двигателя и возмущающего воздействия, соответственно. Численные значения коэффициентов 
, 
собственно и определяют свойства ТРД как объекта регулирования.
Коэффициенты, входящие в уравнение динамики двигателя, положительны. 
- имеет размерность времени, а 
-величина безразмерная.
По своему физическому смыслу постоянная времени характеризует
инерционное запаздывание в изменении числа оборотов двигателя при изменении подачи топлива. Чем меньше постоянная времени, тем быстрее протекает переходный процесс, а следовательно - стабилизация оборотов.
Коэффициент усиления 
характеризует чувствительность двигателя к изменению подачи топлива и фактически связывает обороты с количеством подводимого в двигатель топлива.
Чаще всего указанные характеристики определяются экспериментально
либо по статическим характеристикам конкретного ТРД.
Например, коэффициент усиления 
может быть получен графически
по дроссельным характеристикам, поскольку, как следует из (2.7), на установившемся режиме 
и 
Так как основные
характеристики (дроссельные, высотные, скоростные) получаются на стендах,
при расчетах необходимо предусмотреть приведение данных испытаний к
стандартным атмосферным условиям.
Уравнение ТРД с регулируемым соплом. Для простоты будем считать, что регулируются только обороты. В этом случае вывод уравнения динамики двигателя как объекта регулирования отличается от вывода уравнения (2.5) тем, что избыточный момент является функцией не только числа оборотов, расхода топлива и давления перед компрессорам, но и площади проходного сопла F, т.е. 
. Проводя аналогичные выкладки, получим искомое уравнение
. (2.8)
В уравнении (2.8) постоянные , 
, 
определяются теми же соотношениями (2.5), а
Уравнение одновального ТВД. Для вывода динамической модели
ТВД обозначим через φ угол установки лопастей винта, а избыточный момент 
. Как и ранее, будем предполагать, что регулирование осуществляется по одному параметру - оборотам двигателя.
Тогда, повторяя предыдущие действия (с точностью до обозначений), буден иметь следующее уравнение динамики ТВД
(2.9)
