D arg W1(jw) = 0. (4.2.8)
Условие (4.2.8) выполняется только тогда, когда кривая W1(jw) при изменении частоты от 0 до ∞ не охватывает начала координат комплексной плоскости. Действительно, только в этом случае результирующий поворот вектора W1(jw) при изменении w от 0 до ∞ будет равен нулю, так как возрастание угла j(w), обусловленное движением вектора W1(jw) в положительном направлении (против часовой стрелки), будет компенсироваться таким же убыванием j(w), обусловленным движением вектора W1(jw) в отрицательном направлении (по часовой стрелке).
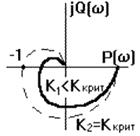
Как видно из (4.2.5), переход на комплексной плоскости от годографа вектора W1(jw) к годографу вектора АФЧХ разомкнутой системы Wpс(jw) осуществляется сдвигом кривой W1(jw) влево на -1, так как Wpc(jw) = W1(jw) -1. С учетом этой операции, получаем следующую формулировку амплитудно-фазового критерия устойчивости Найквиста: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФЧХ разомкнутой системы Wpс(jw) при изменении частоты от 0 до ∞ не охватывает на комплексной плоскости точку с координатами (-1; j0) (рис. 4.2.4, годограф 2).
|
Рис. 4.2.4. |
Более общая формулировка критерия Найквиста относится к системам, имеющим так называемую АФЧХ второго рода (рис. 4.2.4, годограф 1), когда Wpс(jw) пересекает (неограниченное количество раз) вещественную ось левее точки Re Wpc(w) = -1. Будем считать положительным переход годографа через вещественную ось, если он совершается сверху вниз, и отрицательным, если он совершается снизу вверх. Для таких годографов критерий Найквиста формулируется в следующем виде: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменении частоты от 0 до +∞ разность между числом положительных переходов годографа АФЧХ разомкнутой системы через участок вещественной оси (-1; -∞) и числом отрицательных переходов равна нулю. Из этого условия видно, что система, устойчивая в разомкнутом состоянии и имеющая АФЧХ в форме кривой 1 на рис. 4.2.4, устойчива и в замкнутом состоянии.
|
Рис. 4.2.5. |
На рис. 4.2.5а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на рис. 4.2.5б - замкнутая САУ неустойчива.
На рис. 4.2.5в и 4.2.5г показаны АФЧХ разомкнутых астатических САУ, соответственно устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при w ® 0 уходит в бесконечность. В этом случае при использовании критерия Найквиста ее мысленно замыкают на вещественную ось по дуге окружности бесконечно большого радиуса.
Критерий Найквиста нагляден. Он позволяет не только выявить, устойчива ли система, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.
4.3. ЗАПАС УСТОЙЧИВОСТИ СИСТЕМ [7].
Понятие структурной устойчивости. Астатическая система может быть неустойчивой по двум причинам: неподходящий состав динамических звеньев и неподходящие значения параметров звеньев.
Системы, неустойчивые по первой причине, называются структурно неустойчивыми. Это означает, что изменением параметров системы нельзя добиться ее устойчивости, нужно менять ее структуру.
|
Рис. 4.3.1. |
Например, если система состоит из любого количества инерционных и колебательных звеньев, она имеет вид, показанный на рис. 4.3.1. При увеличении коэффициента усиления системы K каждая точка ее АФЧХ удаляется от начала координат, пока при некотором значении Ккрит АФЧХ не пересечет точку (-1, j0). При дальнейшем увеличении K, система будет неустойчива. И, наоборот, при уменьшении K такую систему, в принципе, можно сделать устойчивой, поэтому ее называют структурно устойчивой.
Если система астатическая, то n - порядок астатизма, равен количеству последовательно включенных интеграторов. При ее размыкании характеристическое уравнение системы имеет нулевые корни, поэтому при w®∞ АФЧХ стремится к ∞ (рис. 4.2.5в и 4.2.5г). Например, пусть Wр(p) = K/(p(Tp+1)), тогда АФЧХ разомкнутой системы:
W(jw) =  = P(w) + jQ(w).
= P(w) + jQ(w).
|
Рис. 4.3.2. |
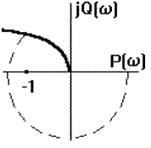
Так как порядок знаменателя больше порядка числителя, то при w®0 имеем P(w)®∞, Q(w)® -j∞. Подобная АФЧХ представлена на рис. 4.3.2. Так как АФЧХ терпит разрыв, трудно сказать, охватывает ли она точку (-1,j0). В этом случае пользуются следующим приемом: если АФЧХ терпит разрыв, уходя в бесконечность при w®0, ее дополняют мысленно полуокружностью бесконечного радиуса, начинающейся на положительной вещественной полуоси и продолжающейся до АФЧХ в отрицательном направлении. После этого можно применить критерий Найквиста. Как видно из рисунка, система, имеющая одно интегрирующее звено, является структурно устойчивой.
|
Рис. 4.3.3. |
Если система имеет два интегрирующих звена (порядок астатизма 2), ее АФЧХ уходит в бесконечность во втором квадранте (рис. 4.3.3). Например, пусть Wр(p) = K/(p2 (Tp+1)), тогда АФЧХ системы:
W(jw) =  = P(w) + jQ(w).
= P(w) + jQ(w).
При w®0 имеем P(w)® -∞, Q(w)® j∞. Такая система не будет устойчива ни при каких значениях параметров, то есть она структурно неустойчива.
Структурно неустойчивую систему можно сделать устойчивой, включив в нее корректирующие звенья (например, дифференцирующие) или изменив структуру системы, например, с помощью местных обратных связей.
Понятие запаса устойчивости. В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать систему так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.
|
Рис. 4.3.4. |
Согласно критерию Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.
Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой системы от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс (рис. 4.3.4).
Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом j между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.
|
Рис. 4.3.5. |
Как уже отмечалось, с ростом коэффициента передачи разомкнутой системы растет модуль каждой точки АФЧХ и при некотором значении K = Kкр АФЧХ пройдет через критическую точку (рис. 4.3.5а) и попадет на границу устойчивости, а при K > Kкр замкнутая система станет неустойчива. Однако в случае АФЧХ типа 1 (рис. 4.2.4) (получаются из-за наличия внутренних обратных связей) не только увеличение, но и уменьшение K может привести к потере устойчивости замкнутых систем (рис. 4.3.5в). В этом случае запас устойчивости определяется двумя отрезками h1 и h2, заключенными между критической точкой и АФЧХ.
|
Рис. 4.3.6. |
Обычно при создании системы задаются требуемыми запасами устойчивости h и j, за пределы которых она выходить не должна. Эти пределы выставляются в виде сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой системы входить не должна (рис. 4.3.6).
|
Рис. 4.3.7. |
Анализ устойчивости по ЛЧХ. Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой системы. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.
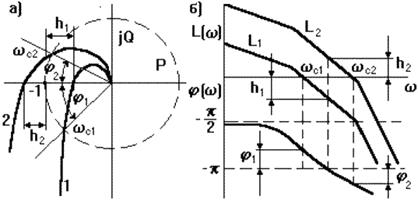
Пусть известны частотные характеристики двух разомкнутых систем (1 и 2), отличающихся друг от друга только коэффициентом передачи K1 < K2. Пусть первая система устойчива в замкнутом состоянии, вторая нет (рис. 4.3.7).
Если W1(p) - передаточная функция первой системы, то передаточная функция второй системы W2(p) = K  W1(p), где K = K2/K1. Вторую систему можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (Безинерционное звено) и W1(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев. Поэтому ЛАЧХ второй системы: L2(w) = 20 lg K + L1(w), а ЛФЧХ: j2(w) = j1(w).
W1(p), где K = K2/K1. Вторую систему можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (Безинерционное звено) и W1(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев. Поэтому ЛАЧХ второй системы: L2(w) = 20 lg K + L1(w), а ЛФЧХ: j2(w) = j1(w).
Пересечениям АФЧХ вещественной оси соответствует значение фазы j = -p. Это соответствует точке пересечения ЛФЧХ j = -p линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A1(w) < 1, A2(w) > 1, что соответствует на ЛАЧХ значениям L1(w) = 20 lg A1(w) < 0 и L2(w) > 0.
Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ j = -p будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h1 и h2, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где j = -p, но в логарифмическом масштабе.
Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты wc1 и wc2, при которых это происходит, называют частотами среза.
В точках пересечения A(w) = 1 = > L(w) = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ jc1 > -p (рис. 4.3.7а кривая 1), то замкнутая система устойчива. На рис. 4.3.7б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии j = -p. И, наоборот, для неустойчивой замкнутой системы (рис. 4.3.7а кривая 2) jc2 < -p, поэтому при w = wc2 ЛФЧХ проходит ниже линии j = -p. Угол j1 = jc1-(-p) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии j = -p до ЛФЧХ.
Исходя из сказанного, критерий устойчивости Найквиста по логарифмическим ЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [-∞; -1], можно сформулировать так: для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию j = -p, была больше частоты среза.
Если АФЧХ разомкнутой системы имеет сложный вид, то ЛФЧХ может несколько раз пересекать линию j = -p. В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.
4.4. ТОЧНОСТЬ СИСТЕМ [8].
Понятие точности является центральным в теории автоматического управления, так как позволяет количественно выразить показатели качества систем. Различают точность, рассматриваемую в переходном процессе - динамическая точность, и точность в установившемся режиме - статическая точность.
|
Рис. 4.4.1. |
Проще всего рассмотреть понятие точности на примере следящей системы. Для этого наилучшим образом применима передаточная функция по ошибке, позволяющая записать сигнал ошибки при любом виде задающего воздействия:
e(p) = We(p) Uзад(p) + Wef(p) f(p).
Статическая точность в следящей системе определяется при гармоническом входном воздействии с использованием передаточной функции по ошибке.
e(p) = Wc(p) Uзад(p), Wc(p) = 1/(1+W(p)).
|
Рис. 4.4.2. |
Рассмотрим логарифмическую частотную характеристику системы в установившемся режиме при гармоническом входном воздействии (рис. 4.4.2). Жирной линией показан идеальный случай абсолютно точной системы. Реальная частотная характеристика отличается от идеальной и в некоторой полосе (wн, wв) не выходит за пределы допуска e. Такое же рассуждение справедливо и для ФЧХ. Задав допустимые границы точности по амплитуде и по фазе, получим область частот, где гарантируется данная точность - это полоса пропускания. Задавая требуемую рабочую частоту по приведенным выше формулам можно вычислить ошибку на этой частоте при гармоническом воздействии.
Общий способ повышения точности (в статическом и динамическом режимах) – обеспечение следующих оценок:
Wзс(p) = W(p)/(1+W(p)» 1 - Мера точности воспроизведения задающего воздействия в замкнутой системе.
Wс(p) = 1/(1+W(p)» 0 - Мера малости ошибки слежения.
Один из основных способов повышения точности - увеличение коэффициента k разомкнутой системы. При увеличении k оба приближённых равенства оценок выполняются всё более точно, что говорит об общем повышении точности, причём это повышение точности происходит при любой W(p).
Однако это не значит, что можно таким образом достичь любой желаемой точности. Здесь начинает сказываться одно из фундаментальных противоречий в рамках теории управления - противоречие между точностью системы и запасом устойчивости. При чрезмерном увеличении k возможна потеря устойчивости замкнутой системы. Годограф Найквиста, не охватывающий точку (-1; j0), но проходящий, например, из 3 квадранта во второй (см., например, кривую 1 на рис. 4.2.4), при увеличении k "раздувается" относительно начала координат и начинает охватывать эту точку, то есть нарушается условие критерия устойчивости Найквиста. Повышение точности всегда приводит к уменьшению запаса устойчивости по амплитуде.
Конкретные значения точности анализируемой системы проводятся разложением We(p) в ряд Тейлора в окрестностях p=0 и анализом коэффициентов этого ряда.
Динамическая точность относится к более сложным задачам анализа систем, т.к. требует изучения всего переходного процесса. При достаточно большом значении модуля АФЧХ в разомкнутой системе передаточная функция прямой ветви имеет пренебрежимо малое значение, передаточная функция замкнутой системы будет в основном определяться цепью ОС. Если коэффициент передачи разомкнутой системы много больше единицы W(p)Woc(p) >>1 и |W(p)| >>1, то для замкнутой системы можно принять:
Wзс(p) = W(p)/(1+W(p)Woc(p))» 1/Woc(p),
что существенно упрощает анализ системы.
Для повышения динамической точности системы обычно используется принцип комбинированного управления по задающему воздействию (принцип инвариантности).
|
Рис. 4.4.3. |
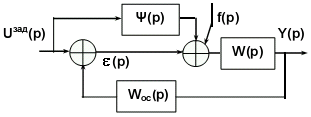
Добавим в стандартную структуру системы дополнительную передаточную функцию Y(p)» 1/(W(p)Woc(p)) так, чтобы сигнал ошибки вообще не зависел от задающего воздействия (рис. 4.4.3). Это можно выполнить введением в систему дополнительной ветви прохождения сигнала, и подобрать коэффициент передачи в этой ветви так, чтобы компенсировать нежелательный сигнал. Аналогичная операция может быть выполнена и на возмущающее воздействие f(p).
4.5. КАЧЕСТВО СИСТЕМ [1, 2, 8, 12].
Показатели качества систем управления. Требование устойчивости для системы относится к числу необходимых, но не может считаться достаточным. Система может быть устойчивой, но время затухания настолько велико или ошибка в установившемся режиме настолько большая, что практически данная система не может быть использована. Поэтому система должна быть не только устойчивой, но иметь определенный переходный процесс, а ошибки в установившихся режимах не должны превышать допустимых.
Характер переходного процесса линейной системы в отличие от устойчивости зависит не только от параметров системы, но и от вида возмущающего (задающего) воздействия и начальных условий. Чтобы сравнивать системы по характеру переходного процесса, из возможных воздействий выбирают типовые или наиболее неблагоприятные и определяют кривую переходного процесса при нулевых начальных условиях. В качестве типовых воздействий обычно принимают единичное ступенчатое воздействие, единичный импульс, линейно нарастающее и синусоидальное воздействие. Для большинства систем наиболее неблагоприятным является воздействие вида единичной ступенчатой функции a(t) =1(t). Реакция системы на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией системы. Для следящих систем обычно рассматривают переходную функцию H(t), вызванную изменением задающего воздействия 1(t), а для систем стабилизации - переходную функцию Hf(t), вызванную изменением возмущающего воздействия f(t).
Точность системы в установившихся режимах оценивается с помощью статических и динамических ошибок. Эти ошибки по аналогии можно назвать показателем качества системы в установившихся режимах. Совокупность показателей качества переходного процесса и установившихся режимов называется показателями качества системы в целом.
Считается, что система обладает требуемым качеством, если ее показатели качества не превышают заданных значений, определенных назначением системы.
|
Рис. 4.5.1 |
Рассмотрим поведение системы управления (рис. 4.5.1), предназначенной для решения задачи слежения - соблюдения заданного закона изменения выходной переменной y(t). Последнее выражается в виде целевого условия
y(t) → у*(t), e(t) → 0, (4.5.1)
e(t) = y*(t) - у(t),
где e(t) - ошибка (рассогласование) системы. При ненулевых начальных рассогласованиях система должна с течением времени обеспечить с некоторой степенью точности совпадение входного (задающего) y*(t) и выходного y(t) сигналов (устранение ошибки e(t)).
Мгновенное устранение возникающих рассогласований e(t) в реальных системах невозможно в силу инерционности систем регулирования и ограничений, накладываемых на управляющие воздействия. Практически неосуществимо и абсолютно точное выполнение асимптотических условий (4.5.1) в силу действующих возмущений и дестабилизирующих факторов. Указанные соображения приводят к необходимости введения специальных показателей качества, характеризующих эффективность решения той или иной задачи управления.
Выходная переменная возмущенной системы определяется суммой свободных и вынужденных составляющих движения:
y(t) = yсв(t) + yв(t),
где в силу устойчивости системы выполняется условия
yсв(t) → 0, yв(t) → yу(t), (4.5.2)
Условия (4.5.2) соответствуют переходному режиму системы, по окончанию которого система "переходит" в установившийся режим yy(t).
В зависимости от свойств системы переходный режим может оказаться достаточно быстрым или медленным, монотонным или колебательным. Для оценки поведения системы в переходном режиме вводятся динамические показатели качества, т. е. численные оценки быстродействия и колебательности системы (время переходного процесса, затухание, перерегулирование, и пр.).
Наиболее просто оценить качество переходного режима автономной системы, для которой вынужденная составляющая отсутствует. В установившемся режиме выходная переменная системы в идеальном случае должна быть идентична задающему воздействию, что соответствует нулевому значению установившейся ошибки.
Существует ряд универсальных приемов, позволяющих одновременно оценить динамические и/или точностные показатели системы, к которым относятся методика оценки качества по переходной функции, оценка по интегральным критериям и т. д.
|
Рис. 4.5.2. |
Показатели качества переходного процесса. Переходная функция системы оценивается с помощью совокупности характеристик, называемых показателями качества переходного процесса. Принято использовать следующие стандартные показатели качества переходного процесса, отражённые на типичном графике 1 переходного процесса в следящей системе со ступенчатым задающим воздействием (рис. 4.5.2):
· tпп - время переходного процесса, по истечении которого отклонение управляемой величины y(t) относительно заданного значения yзад по абсолютному значению становится (и остается в дальнейшем) меньше определенной заданной величины eуст. Обычно принимается eуст = d yзад, d = 0.05. Время регулирования характеризует быстроту затухания переходного процесса.
· tу - время установления, промежуток времени, за который управляемая величина в первый раз достигает своего установившегося значения, характеризует скорость процесса управления.
· eуст - установившаяся ошибка (статическая точность, eуст = e(∞) =1- ууст.). Если eуст=0, то система астатическая.
· σ% - относительное перерегулирование (σ = (ymax-yзад)/yзад). Обычно требуют, чтобы значение σ было менее 18%. Перерегулирование характеризует колебательные свойства процессов. При нулевом значении s процесс носит монотонный характер (график 2 на рис. 4.5.2), а при достаточно больших s приближается к незатухающему колебательному движению.
· n - число колебаний за время переходного процесса (≤3шт.).
Как известно (и следует из выражения (4.1.11), чем дальше полюсы характеристического уравнения системы находятся от границы устойчивости (слева от мнимой оси комплексной плоскости), тем выше скорость протекания переходных процессов в системе. Для количественной оценки быстродействия систем используется также понятие степени устойчивости, которой называется положительное число, соответствующее расстоянию от мнимой оси до ближайшего к ней корня pi:
a = - min Re pi. i = [1, n].
В общем случае, этому условию соответствует пара комплексно сопряженных корней
p1,2 = -a ± jb,
c соответствующей наиболее медленной колебательной составляющей:
yi(t) = A exp(-at) sin(bt+j).
Отсюда, по затуханию колебательного процесса exp(-at) нетрудно определить время переходного процесса по заданной величине d:
tпп ≈ (1/a) ln(1/d).
Знак приближенности в данном случае отражает тот факт, что другие составляющие общего решения (4.1.11) также могут внести определенную долю в значение tпп, особенно, если вещественные части их полюсов близки по значениям к минимальному значению a.
По переходной характеристике и значению установившейся ошибки (ошибки при t>>tпп) можно оценить точность системы в режиме стабилизации - при постоянном входном или заданном воздействии у*(t)=const.
Эти показатели связаны с запасами устойчивости по амплитуде и по фазе. Поэтому, обеспечение стандартных показателей качества обеспечивает необходимую устойчивость. Задачу обеспечения показателей можно рассмотреть как оптимизационную. Как правило, эта задача оказывается многокритериальной и достаточно трудной для решения, в том числе, численного.
При синтезе САУ в системе обычно выделяются неизменяемая часть и изменяемая часть, в которую можно вносить коррективы. Неизменяемая часть системы задает возможность получения гарантированного качества. Классическим методом повышения качества системы является метод диаграмм В.В.Солодовникова. Практическая задача оптимизации обычно выполняется с использованием корректирующих устройств.
Последовательное корректирующее устройство. Передаточная функция разомкнутой скорректированной системы равна исходной, умноженной на передаточную функцию корректора. Корректирующее устройство включается последовательно в контуре системы в любом месте. Для исследования подходят ЛАЧХ, так как они складываются при последовательном соединении. ЛАЧХ и ЛФЧХ корректора находятся в виде разности желаемых и имеющихся частотных характеристик системы.
Типичным последовательным корректирующим устройством является ПИД- регулятор. Эти пропорционально-интегрально-дифференциальные регуляторы выпускаются в широком ассортименте и в разнообразных реализациях, включая программную на контроллерах.
|
Рис. 4.5.3. |
ПИД-регулятор (рис. 4.5.3) имеет три параллельных канала: усилитель с коэффициентом kп, интегратор с коэффициентом kи, дифференциатор с коэффициентом kд. Усилитель позволяет изменить коэффициент усиления системы и уменьшить установившуюся ошибку: eуст =1/(1+kп k). Интегратор повышает порядок астатизма на 1. Увеличение kд повышает запас устойчивости и сглаживает переходный процесс, поэтому дифференциальную составляющую называют демпфированием. С помощью интегральной и пропорциональной составляющих можно обеспечить первый порядок астатизма и желаемую статическую точность в ущерб запасу устойчивости, а дифференциальная составляющая повышает запас устойчивости.
|
Рис. 4.5.4. |
Параллельное корректирующее устройство имеет вид местной отрицательной ОС (рис. 4.5.4). Для синтеза параллельных корректирующих устройств использовать логарифмические частотные характеристики менее удобно, чем для последовательных. Существует ряд инженерных методов расчёта параллельных корректоров (например, метод диаграмм Никольса). Можно просто вычислять корректирующую Wкор(p) по желаемой Wзс(p).
Wкор(p) = (W(p)- Wзс(p))/(W(p)Wзс(p)).
Одна из двух передаточных функций Wкор(p) или Wзс(p) обычно не является физически реализуемой. Тем не менее, всегда можно выбрать достаточно близкую реализуемую функцию.
Метод Солодовникова позволяет построить корректирующее звено для имеющейся системы так, чтобы обеспечит требуемые типовые показатели качества и запас устойчивости по амплитуде и фазе. Метод основан на имеющейся связи между частотной характеристикой и переходной функцией:
H(t) = (2/p)  (P(w)/w) sin(wt) dw,
(P(w)/w) sin(wt) dw,
где P(w) – вещественная часть АФЧХ W(jw)=P(w)+jQ(w).
В.В. Солодовников доказал, что в любой системе имеются следующие зависимости между основными показателями качества переходного процесса и Р(ω).
§ σ% > 18%, если есть "горб", т.е. Рмах > Р0;
§ σ% < 18%, если нет горба;
§ σ% = 0, если производная dP/dω<0 и монотонно убывает. Требование монотонного убывания часто налагает неоправданные ограничения на конструкцию, достаточно обеспечивать σ% < 18%.
 2020-06-12
2020-06-12 140
140