Основы теории управления 6 страница

 Dy(t)= y_п(t) - y(t).

Наблюдатели применяются также в системах управления состоянием, в которых не все переменные состояния могут быть измерены или результаты измерения содержат значительные помехи.

Математическая модель (уравнение) объекта управления может содержать коэффициенты q_j - массо-инерционные, электрические, термодинамические и пр. параметры управляемого процесса и других используемых в САУ устройств. В тех случаях, когда значения параметров изменяются во времени или заранее неизвестны, появляется необходимость в использовании идентификаторов параметров.

Идентификатором называется блок (алгоритм) вида q(t)= Q(у(t), u(t), …), где Q(*) - динамический оператор, предназначенный для оценивания параметров ОУ по имеющейся информации о текущем состоянии у(t) и входном воздействии u(t) объекта, т. е. для расчета в реальном времени значений q(t). Идентификаторы применяются в адаптивных системах управления, в которых параметры регулятора не устанавливаются заранее, а настраиваются в процессе работы. В таких системах часто используются адаптивные алгоритмы управления вида u(t) = U(e(t), у*(t), q(t),...), а вектор оценки q(t) может быть получен с помощью алгоритма идентификации.

3.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА УПРАВЛЕНИЯ [1, 8].

Математической моделью динамической системы принято называть совокупность аналитических выражений и алгоритмов, однозначно определяющих развитие процессов в системе, т. е. ее движение. В зависимости от типа сигналов различаются непрерывные и дискретные модели систем. В зависимости от используемых операторов - линейные и нелинейные, временные и частотные модели. К временным относятся модели, в которых аргументом является время (непрерывное или дискретное). Это дифференциальные и разностные уравнения, записанные в явном виде или в операторной форме. Частотные модели предусматривают использование операторов, аргументом которых является частота соответствующего сигнала.

Аналитические модели вход-выход (ВВ) - это описание связи входных и выходных сигналов динамической системы, которое применяется как для отдельных блоков, так и всей системы управления в целом. Для обозначения входных и выходных сигналов воспользуемся обозначениями, характерными для объекта управления, где входным сигналом является управляющее воздействие u(t), а выходным регулируемая переменная y(t). В этом разделе рассматриваются непрерывные временные модели, описывающие связи входных и выходных переменных динамической системы с помощью обыкновенных дифференциальных уравнений соответствующего порядка.

Система линейных уравнений объекта. В общем случае модель одноканального объекта управления описывается нелинейным дифференциальным уравнением (системой уравнений), связывающим входной сигнал управления u(t) и выходной сигнал состояния объекта y(t):

F(y', y", …, y⁽ⁿ⁾, u', u", …, u^(m)) = 0.                                  (3.2.1)

Уравнение описывает динамическое состояние ОУ на некотором временном интервале t≥t_o, и связывает входные сигналы u(t) и их производные u⁽ⁿ⁾(t) с выходными сигналами y(t) и их производными y⁽ⁿ⁾(t). Значения у(t_o) = у_о, у'(t_o) = у'_о,..., y⁽ⁿ⁾(t_o) = у⁽ⁿ⁾_о называются начальными значениями (условиями), а число г = n-m ≥ 1- относительной степенью модели.

Классом дифференциальных уравнений, удобным для проведения исследований, являются линейные дифференциальные уравнения. Переход к линейным дифференциальным уравнениям выполняется операцией линеаризации, при которой переменные уравнения (3.2.1) заменяются новыми переменными – отклонениями от некоторого номинального режима (y=y-y_н, u= u-u_н), начало координат переносится в точку номинального режима, а функция F раскладывается в ряд Тейлора в окрестностях этой точки по частным производным. В результате линеаризации получаем следующую систему линейных уравнений в отклонениях:

A₀(t)y⁽ⁿ⁾ + A₁(t)y^(n-1) +…+ A_n(t)y = B₀(t)u^(m) + В₁(t)y^(m-1) +…+ B_m(t)u.      (3.2.2)        

Порядок системы уравнений равен n по порядку производной y⁽ⁿ⁾(t), n ≥ m, так как при n < m системы технически нереализуемы. Так как все частные производные представляют собой либо постоянные матрицы, либо матрицы, зависящие только от времени, то полученное уравнение есть либо система линейных дифференциальных уравнений с постоянными коэффициентами (A_j(t) = a_j = const, B_j(t) = b_j = const), либо система с переменными коэффициентами, в зависимости от номинальной траектории.

В случае постоянных коэффициентов система называется стационарной. Как правило, входные и выходные величины объекта - скалярные функции, при этом уравнение (3.2.2) принимает вид:

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = b₀u^(m) + b₁y^(m-1) +…+ b_mu.           (3.2.3)         

где a_j, b_j – постоянные коэффициенты (параметры) модели, a₀ > 0, b₀ > 0, n - порядок модели, 0 ≤ m < n. Решение уравнений таких стационарных объектов относительно y(t) является главным объектом исследований в классической теории автоматического управления.

Система, для которой u(t)≡ 0, называется автономной. Описание автономной системы дается однородным дифференциальным уравнением вида

a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = 0.                                   (3.2.3')        

Передаточная функция системы. Основной метод исследования линейных систем с постоянными коэффициентами - преобразование Лапласа. При нулевых начальных условиях, после преобразования Лапласа уравнения вида (3.2.3), получаем:

L[a₀y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny] = L[b₀u^(m) + b₁y^(m-1) +…+ b_mu].

(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n)Y(p) = (b₀p^(m) + b₁p^(m-1) +…+ b_m)U(p).          (3.2.4)

Y(p) = L[y(t)] = exp(-pt) y(t) dt,

U(p) = L[u(t)] = exp(-pt) u(t) dt.

Для линейного уравнения преобразование Лапласа отношения выходного сигнала Y(p) к входному сигналу U(p) при нулевых начальных условиях не зависит от самих сигналов и называется передаточной функцией системы W(p).

Y(p) = U(p) (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n),

W(p) = (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n),           (3.2.5)

Y(p) = W(p) U(p).

Передаточная функция W(p) зависит только от самих дифференциальных уравнений и обладает свойством линейности:

Если Y(p) = Y₁(p) + Y₂(p), то U(p) = W(p)Y₁(p) + W(p)Y₂(p) = U₁(p)+U₂(p).

Если Y(p) = сY(p), то U(p) = W(p) Y(p) = с W(p) Y(p).

В общем случае замкнутая система регулирования с обратной связью рассматривается в структурной форме, приведенной на рис. 3.2.1, где используются следующие обозначения сигналов:

Y(p) = W(p)e(p); W(p) = W₁(p)W₂(p);

Y_ос(p) = W_ос(p)Y(p); e(p)=U(p)-Y_oc(p).

Рис. 3.2.1.

Выражение выходного сигнала состояния системы через входной сигнал управления:

Y(p)=W(p)(U(p)-W_ос(p)Y(p);

Y(p)(1± W(p)W_ос(p))=W(p)U(p).

Отсюда главная передаточная функция замкнутой системы:

W_зс(p) = Y(p)/U(p) = W(p)/[1 ± W(p) W_oc(p)].

Знак плюс или минус определяется типом обратной связи (отрицательная или положительная). Соответственно, выходной сигнал с учетом сигнала дестабилизирующего воздействия f(t), который суммируется с правой частью выражения (3.2.3):

Y(p)=W_зс(p)U(p) + W_f(p)f(p), 

где W_f(p) – передаточная функция по возмущению. В замкнутой системе передаточная функция по возмущению определяется как отношение выходной величины, преобразованной по Лапласу, к функции возмущающего воздействия, преобразованной по Лапласу при нулевых начальных условиях. Возмущающее воздействие может быть приложено к любой точке системы.

W_f(p) = Y(p)/f(p) = W₂(p)/[1+W_oc(p)W(p)].

Передаточная функция по ошибке:

W_e(p) = e(p)/U(p) = 1/[1 + W(p) W_oc(p)].

Передаточная функция по ошибке - основное средство исследования точности САУ. C учетом возмущающего воздействия:

e(p)=W_e(p)U(p) + W_ef(p)f(p),

где W_ef(p) - передаточная функция по ошибке и возмущению (от возмущения к ошибке):

W_ef(p) = e(p)/f(p) = -W₂(p)W_oc(p)/[1 + W(p) W_oc(p)].

Передаточная функция по обратной связи:

W_Yoc(p) = Y_oc(p)/U(p) = W(p) W_oc(p)/[1 + W(p) W_oc(p)].

Типовые звенья САУ. Полиномы числителя и знаменателя передаточной функции (3.2.5) можно разложить на простейшие множители по их корням:

W(p) = N(p)/P(p) = m [(p-p₁^ч)…(p-p_m^ч)] / [(p-p₁^з)…(p-p_n^з)],        (3.2.6)

где μ = b₀ /a₀ – константа, p_i^ч – множество корней числителя N(p)=0, p_i^з – множество корней знаменателя P(p)=0. Корни числителя передаточной функции называют нулями, корни знаменателя – полюсами. Комплексно сопряженные корни объединяются в квадратурные полиномы с вещественными коэффициентами: (p-α+jβ)(p-α-jβ) = p²-2αp+β²+α².

После такого представления в числителе и знаменателе будет некоторое количество скобок первого и второго порядка с вещественными числовыми коэффициентами, каждую из которых можно рассматривать, как элементарную передаточную функцию, практически реализуемую в силу вещественности коэффициентов. Если вынести из всех скобок свободные члены и объединить их произведение в общий множитель К, то получим уравнение:

W(p) = K [W₁(p)…W_z(p)],                                  (3.2.7)

где z=n+m, если все корни вещественные, z < n+m, если есть комплексные корни. Коэффициент К принято называть коэффициентом усиления системы. Заметим, что W(0) = К = b_m/a_n, т.е. его числовое значение равно коэффициенту усиления на нулевой частоте ("постоянном токе").

       Классификация звеньев производится по виду их передаточных функций, независимо от исполнения (механические, гидравлические, электрические и пр.). Передаточные функции типовых звеньев, из которых синтезируются системы, обычно имеют числитель или знаменатель, равный единице. Ниже приводятся выражения передаточных функций основных типовых звеньев систем:

1. К - Усилительное звено.

2. p - Дифференцирующее звено.

3. 1/p - Интегрирующее звено (интегратор).

4. K/(Tp+1) - Инерционное (апериодическое) звено.

5. K/(T²p+2dTp+1) - Колебательное звено.

6. K(Tp+1) - Форсирующее звено.

7. K(T²p+2dTp+1) - Форсирующее звено 2-го порядка.

Здесь Т – определенный временной коэффициент (постоянная времени). Звенья 2, 6 и 7 не реализуются в строгом теоретическом смысле, существуют только их приближения.

Типовые входные воздействия. Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия. Наиболее распространенными типовыми воздействиями являются ступенчатое, импульсное и гармоническое. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий u_i(t) и на основании принципа суперпозиции получить результирующее изменение выходной величины y(t) в виде суммы реакций системы на каждую из составляющих.

Рис. 3.2.1.

Единичная ступенька.  Особое значение в теории автоматического управления имеет ступенчатое воздействие 1(t) = 1 при t≥0, 1(t) = 0 при t<0 (сигнал u₁(t) на рис. 3.2.1). Все остальные воздействия могут быть сведены к нему. Так, например, импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой величины противоположными по знаку, поданными один за другим через интервал времени Dt(сигнал u(t) на рис. 3.2.1).

Преобразование Лапласа для единичной ступеньки:

1(p) = exp(-pt) dt = 1/p.                (3.2.8)

Линейно нарастающее воздействие (t(t)=t при t≥0, t(t) = 0 при t<0) представляет собой интеграл по времени от единичной ступеньки:

t(t) = 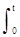1(t) dt, 1(t) = d t(t) /dt.

Преобразование Лапласа:

t(p) = t exp(-pt) dt = 1/p².                (3.2.9)

Экспоненциальная функция exp(at). Преобразование Лапласа:

L[exp(at)] = exp(at) exp(-pt) dt = 1/(p-a).               (3.2.10)

Выражение справедливо и при любом комплексном α.

Гармонические воздействия sin ωt и соs ωt. 

На основе формулы Эйлера exp(jωt) = cos ωt + j sin ωt соответственно имеем cos ωt = Re exp(jωt), sin wt = Im exp(jwt). Преобразования Лапласа:

L[sin ωt] = L[Im e^jωt] = Im L[e^jωt] = Im (1/(p-jω)) = Im((p+jω)/(p²+ω²)) =

= Im(p/(p²+ω²)+jω/(p²+ω²)) = ω/(p²+ω²).

L[cos ωt] = Re L(e^jωt) = Re (1/(p-jω)) = Re((p+jω)/(p²+ω²)) = p/(p²+ω²).

Дельта - функция δ(t) - математическая модель очень короткого конечного воздействия большой мощности (единичный импульс). Определение δ(t)-функции даётся через интеграл свёртки с любой другой интегрируемой функцией x(t):

d(t-t₀) x(t) dt = x(t₀).

Отсюда, при x(t)=1:

d(t) dt = 1, d(t) exp(-pt) dt = 1, L[d(t)] = 1.       (3.2.11)

Единичный импульс физически представляет собой очень узкий импульс, ширина которого стремится к нулю, а высота - к бесконечности, ограничивающий единичную площадь. Дельта - функция связана с единичной ступенчатой и линейно-нарастающей функцией выражением:

d(t) = d1(t) /dt = d² t(t) /dt².

3.3. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ САУ [7, 8].

Понятие временных характеристик. Зависимость изменения выходной величины системы от времени при подаче на ее вход единичного воздействия (импульса Дирака) при нулевых начальных условиях называется импульсным откликом системы или импульсной переходной характеристикой h(t). Эту функцию называют также функцией веса. Так как системы управления являются физически реализуемыми системами, импульсный отклик систем является односторонней каузальной функцией (h(t)=0 при t<0).

Как известно из теории сигналов и систем, отклик системы на единичный импульс определяется сверткой:

h(t) ③ d(t) =  h(t) d(t-t) dt = h(t).

Выходной сигнал в каждый момент времени t_i зависит не только от входного сигнала в этот момент времени, но и от сигналов на входе во все предыдущие моменты времени t_i-t с “весом”, равным значениям функции h(t), т.е. в данном случае от сигнала d(t) при t=0.

Преобразование Лапласа свертки функций отображается произведением их изображений:

h(p) = W(p) L[d(t)] = W(p) 1 = W(p).                             (3.3.1)

В действительности дельта-функция в чисто теоретическом плане не реализуется. Реальные импульсные воздействия на системы всегда конечны по величине и продолжительности. Но если их продолжительность достаточно мала по сравнению со временем переходного процесса в системе (длительностью переходной характеристики в пределах заданной погрешности), то входное воздействие можно считать приближением к дельта-функции и применять для оценки переходных процессов в системе.

Не меньшее значение в САУ уделяется переходной характеристике H(t), реакции системы на единичное ступенчатое воздействие. Изображение Лапласа:

H(p) = W(p)/p.                                              (3.3.2)

Переходная и импульсная переходная характеристики называются временными характеристиками. Каждая из них является исчерпывающей характеристикой системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно определить выходную величину при произвольном входном воздействии.

Экспериментальное определение временных параметров системы и отдельных ее звеньев можно проводить подачей единичных импульсных сигналов или единичных ступеней на их входы с измерением реакции на выходах. Если на вход подать d(t) ≈ d(t) и зарегистрировать на выходе h_d(t) ≈ h(t), то изображение Лапласа передаточной функции определится выражением:

L[h_d(t)] = W_d(p) ≈ W(p).

       Соответственно, при подаче на вход ступенчатой функции 1(t) регистрируется переходная функция H(t) и вычисляется W(p):

W(p) = L[dH(t)/dt].

       Для произвольного входного воздействия u(t) при t≥0 переходной процесс на выходе звена при известных функциях H(t) или h(t) и нулевых начальных условиях:

y(t) = u(0)H(t) + H(t) u(t-t) dt, y(t) = h(t) u(t-t) dt.

Физическая реализуемость. Передаточная функция является физически реализуемой, если возможно создание устройства или программы, которые позволяют реально получить или вычислить выход блока с такой передаточной функцией для реальных типовых входных сигналах и их комбинаций. На выходе систем не должно появляться стремящихся к бесконечности значений сигналов в конечные моменты времени при подаче на вход конечных сигналов.

Заведомо физически нереализуемой является передаточная функция (3.2.5) с порядком числителя большим порядка знаменателя. Строго говоря, физически нереализуемой является и функция с порядком числителя равным порядку знаменателя. В первом случае после деления числителя на знаменатель выделяется, помимо прочего, несколько идеальных дифференцирующих звеньев. Во втором случае при делении числителя на знаменатель выделяется усилительное звено. Заметим, что даже идеальный усилитель не может быть физически реализован, не говоря уже об идеальном дифференцирующем звене, так как в обоих случаях частотная характеристика системы не стремятся к нулю на больших частотах.

3.4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ САУ [7, 8, 9, 14].

Понятие частотных характеристик является важнейшим понятием, широко применяемым в теории управления. Методы, основанные на применении частотных характеристик, являются наиболее удобными в инженерной практике в классе систем с одним входом и выходом.

Функция W(jw), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Она может быть получена путем замены p на jw в выражении W(p). В более общей формулировке частотную передаточную функцию можно представить в виде отношения частотных спектров выходного и входного сигнала:

W(jw) = Y(jw)/U(jw) = W(p)|_p=jw.

Частотная передаточная функция линейного звена является изображением Фурье его импульсной функции и может определяться по интегральному преобразованию:

W(jw) = h(t) exp(-jwt) dt.

Для односторонних функций h(t), W(jw) есть комплексная функция, которую иногда называют амплитудно-фазо-частотной характеристикой (АФЧХ):

W(jw) = A(w) exp(jj(w)) = P(w) + jQ(w),

где P(w) - вещественная, Q(w) - мнимая частотные характеристики, А(w) - амплитудная частотная характеристика (АЧХ), j(w) - фазовая частотная характеристика (ФЧХ). АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной:

A(w) = U_m /Y_m = |W(jw)| = ,

j(w) = arctg(Q(w)/P(w)).

Рис. 3.4.1.

Годограф, приведенный на рис. 3.4.1, является стандартным методом отображения АФЧХ на комплексной плоскости с координатами ReW(ω) и ImW(ω). Параметром на кривой годографа является частота, изменяющаяся в интервале от 0 до ∞. Для произвольной частоты ω радиус вектор в точке W(jω) показывает амплитуду выходного сигнала, а угол j(ω) - сдвиг фазы между выходным и входным сигналом. Иногда W(jω) называют комплексным коэффициентом передачи, подразумевая, что АФЧХ является обобщением обычного коэффициента усиления К на случай его зависимости от частоты и фазового сдвига, также зависящего от частоты. Комплексно сопряженные ветви АФЧХ, отличающиеся знаком j, зеркальны относительно вещественной оси.

Для частотного анализа систем применяется также раздельное построение графиков АЧХ и ФЧХ, если в том появляется необходимость.

Логарифмические частотные характеристики. В практике автоматики широкое применение находят частотные характеристики в логарифмических масштабах. Применение логарифмического масштаба позволяет наглядно изображать характеристики в большом диапазоне частот, представлять характеристики отрезками ломанных линии и определять характеристики сложных систем простым суммированием характеристик, входящих в эти системы элементов.

Частота в логарифмическом масштабе измеряется в декадах. Две частоты w₁ и w₂ отличаются на одну декаду если w₂/w₁ = 10, lg(w₂/w₁) = 1. Относительные амплитуды в логарифмическом масштабе выражаются в децибелах. Две мощности w₁ и w₂ отличаются на один децибел, если 10 lg(w₁/w₂) = 1. Так как мощности относятся как квадраты образующих их первообразных (напряжений, токов, сил и т.д.), то две первообразные a₁ и а₂ будут отличаться на один децибел, если 10 lg(а₁² /а₂²) = 1 ® 20 lg(а₁/а₂) = 1. 

В CАУ широко используются логарифмические амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) частотные характеристики (рис. 3.4.2). Они получаются путем логарифмирования передаточной функции:

lg[W(jw)] = lg[A(w) exp(jj(w)] = lg[A(w)]+lg[exp(jj(w)] = L(w) + j(w).

ЛАЧХ получают из первого слагаемого, которое умножается на 20, то есть L(w)=20 lg A(w). Величина L(w) откладывается по оси ординат в децибелах. Изменению сигнала в 10 раз соответствует изменение его уровня на 20 дБ. По оси абсцисс откладывается частота w в логарифмическом масштабе, единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз.

Рис. 3.4.2.

ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси w. Величина j(w) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -p ≤ j ≤ p.

Частотные характеристики являются исчерпывающими характеристиками системы, по которым можно восстановить ее передаточную функцию и определить параметры.

3.5. ХАРАКТЕРИСТИКИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ СИСТЕМ [1, 7, 8, 9].

Элементарными звеньями называются простейшие составные части (блоки) системы, поведение которых описывается алгебраическими уравнениями или дифференциальными уравнениями (1-2)-го порядков:

a₀ y"(t) + a₁ y'(t) + a₂ y(t) = b₀ u'(t) + b₁ u(t).                            (3.5.1)

Передаточная функция элементарного звена имеет вид:

W(p) = (b₀ u'(t) + b₁ u(t)) / (a₀ y"(t) + a₁ y'(t) + a₂ y(t)).                    (3.5.2)

Безынерционное (пропорциональное, усилительное) звено, для которого в любой момент времени выходная величина пропорциональна входной. И в статике, и в динамике описывается уравнением:

y(t) = k u(t).

Безинерционное звено передаст сигнал без искажения по форме и сдвига во времени, но измененный по амплитуде в k раз. Реальные звенья могут быть отнесены к данному типу условно, так как всегда обладают инерционностью. Однако если переходный процесс в элементах звена протекает за время, малое по сравнению с временем переходного процесса системы в целом, то эти элементы могут считаться безинерционными. 

Рис. 3.5.1.

Динамический параметр k называют коэффициентом усиления. Переходная  характеристика повторяет   ступенчатое входное воздействие 1(t), измененное (увеличенное или уменьшенное) в k раз (рис. 3.5.1):

H(t) = k 1(t).

При k = 1 звено передает входной сигнал на выход, а при k = -1 инвертирует входной сигнал. Передаточная функция звена равна коэффициенту пропорциональности:

W(p) = k.

       Функция веса представляет собой импульсную функцию, площадь которой равна k:

h(t) = k d(t).

Рис. 3.5.2.

Амплитудно-фазо-частотная характеристика АФЧХ: W(jw) = k. АЧХ: A(w) = k. ФЧХ: j(w) = 0. ЛАЧХ: L(w) = 20 lg k.

Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе (рис. 3.5.2).

Некоторые реальные звенья могут рассматриваться как безинерционные с определенной точностью (жесткий механический рычаг, механический редуктор, потенциометр, широкополосный электронный усилитель и т.п.). Многие датчики сигналов (потенциометрические, индукционные и пр.) также обычно рассматриваются как безынерционные.

Апериодическое инерционное звено первого порядка описывается дифференциальным уравнением: T dy/dt + y(t) = k u(t). Передаточная функция звена: W(p) = k/(Tp+1).

Динамические свойства определяются значениями двух величин, k и Т. Т – постоянная времени, k – коэффициент передачи (усиления) звена. Переходная функция:

H(p) = W(p) 1(p) = k/[p(Tp+1)].

       При обратном преобразовании Лапласа функции Н(р) по формуле вычетов:

H(t) = k (1-exp(-t/T)

Рис. 3.5.3.

Переходный процесс инерционного звена экспоненциальный - типичный для систем первого порядка (рис. 3.5.3). Выходная величина звена в переходном режиме со скоростью, определяемой величиной Т, следует за изменением входной величины (свойство инерционности). Сигнал на выходе звена нарастает по экспоненте, поэтому звено называют апериодическим. При t→∞ сигнал стремится к значению k.