Дифракция Френеля на круглом отверстии

Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса 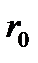 ( рис.7 ).

Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.

При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.

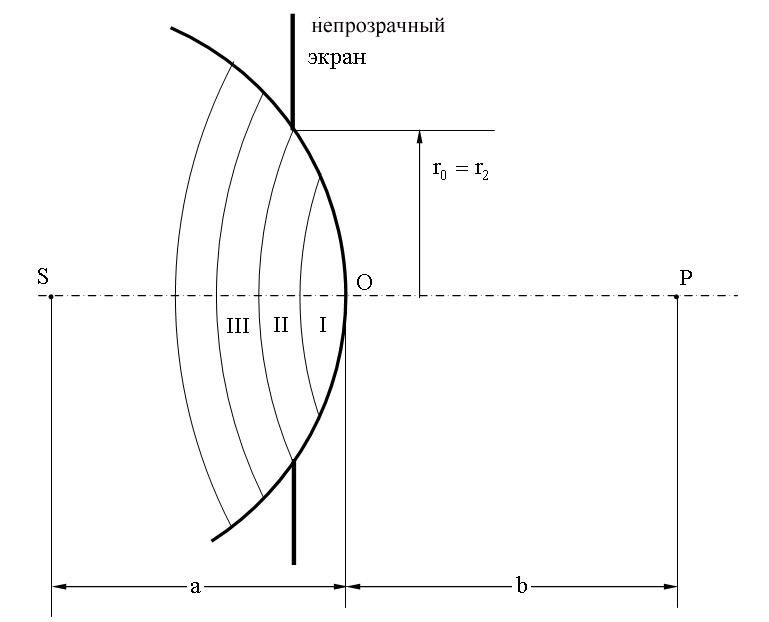
Рис.7. Дифракция Френеля на круглом отверстии

Можно показать, что радиус зоны Френеля с номером 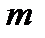 при не очень больших :                                                               

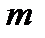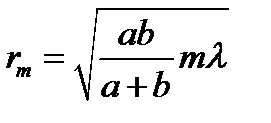(7)

Расстояние примерно равно расстоянию от источника до преграды, расстояние 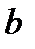– от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля, то, приравняв 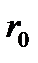и 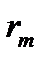, получим формулу для подсчета числа открытых зон Френеля:      

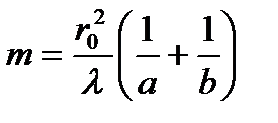(8)

При 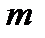четном в точке P будет минимум интенсивности, при нечетном – максимум (рис.8).

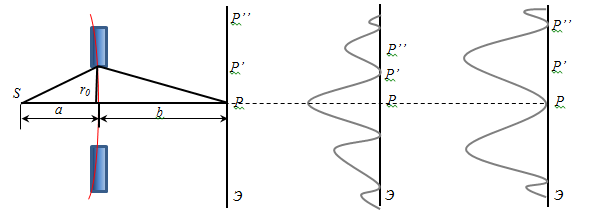
Рис.8. Распределение интенсивностей при дифракции Френеля на круглом отверстии

Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных колец, причем к центре будет светлое пятно (максимум), если в отверстии укладывается нечетное число зон Френеля, либо темное, если укладывается четное число зон Френеля.

Если 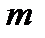< 1, то на экране будет размытое светлое пятно.

Если 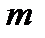→∞, то дифракционная картина будет наблюдаться на границе геометрической тени.