Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз (рис. 6). Таким образом, получаются два луча.
Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает.
При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.

Рис. 6. Интерференция на тонких пластинках
Для  и
и  оптическая разность хода
оптическая разность хода  . После преобразований с учетом закона преломления и тригонометрических формул получим:
. После преобразований с учетом закона преломления и тригонометрических формул получим:

 (27)
(27) 
Если  , тогда:
, тогда:
 (28)
(28)
Здесь  появилась за счет изменения фазы волны на противоположную при отражении в точке А.
появилась за счет изменения фазы волны на противоположную при отражении в точке А.
Кольца Ньютона
Интерференционная картина, образованная отраженными под разными углами плоскими волнами от поверхностей плоскопараллельной пластинки, получила название интерференционных полос равного наклона.
Другой вид интерференции света в тонких пленках, толщина которых меняется по поперечному сечению, получил название интерференционных полос равной толщины. Частным случаем полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 7). Роль тонкой пленки, от поверхности которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. При нормальном падении света полосы равной толщины имеют вид окружностей. Заметим, что центр колец Ньютона, наблюдаемых в отраженном свете, оказывается темным. При освещении системы монохроматическими лучами в отраженном свете наблюдаются перемежающиеся светлые и темные кольца. Если использовать белый свет, то светлые кольца становятся окрашенными, так как для одних длин волн выполняется условие интерференционного максимума, а для других - минимума.

Рис. 7. Получение колец Ньютона
Интерференция наблюдается не только в отраженном, но и в проходящем сквозь пленку свете, причем максимумам интерференции в отраженном свете соответствуют минимумы в проходящем свете, и наоборот.
При вычислении оптической разности хода лучей 1 и 2 вследствие малости толщины воздушного зазора можно пренебречь наклоном луча 2 в нем. Тогда геометрическая разность хода равна 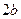 , где
, где  – толщина воздушного зазора в данном месте (рис.8). Показатель преломления воздуха считаем равным единице, поэтому оптическая разность хода совпадает с геометрической. При вычислении полной оптической разности хода нужно учесть, что при отражении от оптически более плотной среды фаза светового вектора меняется на
– толщина воздушного зазора в данном месте (рис.8). Показатель преломления воздуха считаем равным единице, поэтому оптическая разность хода совпадает с геометрической. При вычислении полной оптической разности хода нужно учесть, что при отражении от оптически более плотной среды фаза светового вектора меняется на  , а при отражении от оптически менее плотной среды фаза светового вектора не меняется. Разность фаз
, а при отражении от оптически менее плотной среды фаза светового вектора не меняется. Разность фаз  эквивалентна оптической разности хода
эквивалентна оптической разности хода  .
.
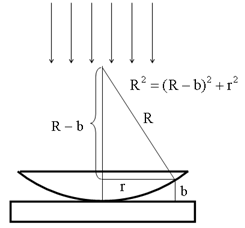
Рис.8. К выводу формулы для радиусов колец Ньютона
Полная оптическая разность хода равна:
 (29)
(29)
Линии постоянной оптической разности хода представляют собой концентрические окружности с центром в точке соприкосновения линзы и пластинки. При заданном значении длины волны  оптическая разность хода
оптическая разность хода  зависит только от толщины воздушного зазора. Интерференционные полосы являются, таким образом, полосами равной толщины.
зависит только от толщины воздушного зазора. Интерференционные полосы являются, таким образом, полосами равной толщины.
Связь между  ,
, 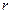 и
и  нетрудно найти из геометрических соображений:
нетрудно найти из геометрических соображений:
 (30)
(30)
Ввиду того, что 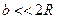 величиной
величиной  можно пренебречь по сравнению с
можно пренебречь по сравнению с 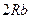 :
: 
 . Отсюда получим, что
. Отсюда получим, что
 (31)
(31)
Таким образом, полная оптическая разность хода дается выражением:
 (32)
(32)
В точках, для которых
 , (33)
, (33)
возникнут максимумы; в точках, для которых
 (34)
(34)
Выведем формулу для радиусов светлых колец, приравняв выражение (32) для оптической разности хода и условие интерференционного максимума (33):
 (35)
(35)
После преобразований (36), (37) получим формулу для радиусов светлых колец (38):
 (36)
(36)
 (37)
(37)
 (38)
(38)
Аналогичным образом получается выражение (42) для радиусов темных колец:
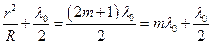 (39)
(39)
 (40)
(40)
 (41)
(41)
 (42)
(42)
 2020-06-12
2020-06-12 325
325








