Интерференция от двух монохроматических источников одинаковой частоты

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Им. Ф.М. ДОСТОЕВСКОГО

ИНТЕРФЕРЕНЦИЯ СВЕТА

Учебно-методическое пособие по курсам «Оптика» и «Общий физический практикум»

Омск

2019

Рецензенты:

 

К.ф.-м.н. Н.А. Давлеткильдеев (КНИОРП ОНЦ СО РАН)

К.ф.-м.н., Г.М. Серопян (ФГБОУ ВО ОмГУ им. Ф.М. Достоевского)

 

Интерференция света: учебно-методическое пособие по курсам «Оптика и «Общий физический практикум»/ авт.: Б.Т. Байсова, Л.В. Баранова.– Омск: изд-во Ом.гос.ун-та, 2019.–39 с.

 

 

В пособии представлены краткие теоретические сведения по разделу волновой оптики «Интерференция света», обеспечивающие выполнение цикла лабораторных работ. Пособие также включает в себя лабораторный практикум и представляет собой самостоятельное руководство к лабораторным занятиям для студентов физического факультета. Практикум содержит описание выполнения трех лабораторных работ по курсам «Оптика» и  «Общий физический практикум».

Предназначено для обучающихся по направлениям подготовки бакалавров 03.03.02 «Физика», 03.03.03 «Радиофизика».  

 

Настоящее пособие представляет собой самостоятельное руководство к практическим занятиям для студентов физического, химического факультетов, факультета компьютерных наук. Настоящий лабораторный практикум посвящен ознакомлению с явлением интерференции. В представленном теоретическом материале рассмотрены основные условия наблюдения интерференции света, способы получения когерентных источников в оптике, расчет интерференционной картины (опыт Юнга), интерференция в тонких пленках. Практикум содержит описание 5-ти лабораторных работ по курсу «Оптика», и методические указания по обработке и анализу экспериментальных данных.

 

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ……………………………………………………………….…4

ГЛАВА 1. Основные теоретические сведения……………………...…………..5

1.1. Интерференция света…………………………………………………………5

1.2. Интерференция от двух монохроматических источников одинаковой частоты……………………………………………………………...…………6

1.3. Условия максимума и минимума интерференции………………………….8

1.4. Получение когерентных волн в оптике……………………………………..9

1.4.1. Опыт Юнга…………………………………………………………..…….…10

1.4.2. Зеркала Френеля…………………………………………………..…………11

1.4.3. Бипризма Френеля…………………………………………….……………..11

1.5. Интерференция при отражении от прозрачных пластинок……………………………………………………………..……...12

1.6. Кольца Ньютона……………………….……………………………..….…..13

1.7. Интерференционные полосы равного наклона……………………………16

ГЛАВА 2. Лабораторный практикум…………..……………………………....18

2.1. Определение длины световой волны с помощью колец Ньютона……….18

2.2. Определение длины световой волны с помощью бипризмы Френеля…………………………………………………………………….……….22

2.3. Определение толщины пластинки с помощью наблюдения интерференционных полос равного наклона.........................................................27

2.4. Измерение показателей преломления жидкостей с помощью интерферометра Релея……………………………………………………………29

2.5. Изучение интерференции поляризованных лучей………………………33

СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………………………………………………..……………….…39

ПРЕДИСЛОВИЕ

Целью настоящего учебно-методического пособия является ознакомление студентов с основными теоретическими сведениями по теме «Интерференция света» с последующим закреплением теории на практике при выполнении цикла лабораторных работ.

Пособие способствует формированию у студентов практических навыков работы на оптическом оборудовании с возможностью наглядного наблюдения изучаемых явлений  с последующим оформлением результатов эксперимента.    

В первой главе изложены краткие теоретические сведения. В представленном теоретическом материале рассмотрены основные условия наблюдения интерференции света, способы получения когерентных волн в оптике, расчет интерференционной картины, интерференция в тонких пленках. Во второй главе представлен лабораторный практикум, включающий пять работ: «Определение длины световой волны с помощью колец Ньютона», «Определение длины световой волны с помощью бипризмы Френеля», «Определение толщины пластинки с помощью наблюдения интерференционных полос равного наклона», «Измерение показателей преломления жидкостей с помощью интерферометра Релея», «Изучение интерференции поляризованных лучей». По каждой работе представлены методические указания о порядке ее выполнения, описание лабораторных установок,  а также перечень контрольных вопросов и список рекомендуемой литературы.

 

ГЛАВА 1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Интерференция света

Интерференция света – это явление наложения когерентных волн, при котором происходит пространственное перераспределение энергии, то есть появление максимумов и минимумов интенсивности в разных точках пространства.В переводе с латинского языка интерференция означает «взаимодействие» (от лат. Inter - взаимно, ferio - ударяю) – взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.

Условия интерференции:

 Интерферировать могут только когерентные волны. Все источники света, кроме лазера, некогерентны, поэтому интерференционную картину невозможно получить с помощью обычных источников, например, электрических лампочек. Включение еще одной лампочки приводит к увеличению освещенности поверхности, а не к чередованию максимумов и минимумов освещенности.

Когерентные волны – волны, которые имеют одинаковую частоту, длину волны и постоянную в течение времени наблюдения разность фаз. Для волн, имеющих одинаковую частоту, разность фаз всегда постоянна. Однако у всех естественных источников фазы хаотически меняются с очень большой частотой, вследствие этого разность фаз двух независимых источников, также хаотически меняется во времени. Это приводит к тому, что максимумы и минимумы (светлые и темные участки) будут перемещаться в поле зрения наблюдателя. Приемники излучения (глаз, термоэлемент и т.п.) не могут с такой быстротой следить за изменением освещенности интерференционной картины и будут воспринимать среднюю во времени освещенность без всяких максимумов и минимумов. В этом случае имеет место простое сложение интенсивностей обоих источников.

Основная трудность в осуществлении интерференции света состоит в получении когерентных световых волн. На основании рассмотрения особенностей процесса излучения тепловых источников света можно сделать вывод, что излучение даже двух атомов таких источников не будет когерентно. Следовательно, невозможно получить интерференционную картину путем сложения излучений различных частей теплового источника света. Интерференционные явления при использовании тепловых источников света будут иметь место в том случае, если каким-либо способом поделить на две (или больше) частей излучение каждого волнового цуга и таким образом сформировать две системы волн.

В настоящее время наибольшей монохроматичностью (когерентностью) обладают лазерные источники излучения. Отличие процессов излучения в лазерах и тепловых источниках заключается в том, что в лазерах излучения атомов являются не спонтанными, а носят вынужденный характер и все излучающие атомы жестко связаны по фазе, этим и обусловливается их когерентность.

Таким образом, экспериментально можно получить когерентные пучки из одного светового пучка двумя способами: методом деления волнового фронта и методом деления амплитуды.

 

 

Интерференция от двух монохроматических источников одинаковой частоты

Пусть в точках S₁ и S₂ находятся источники световых волн, которые излучают монохроматические волны одинаковой частоты. Эти волны перекрываются в окружающем источники пространстве. Найдем результат перекрывания волн в точке Р, отстоящей от первого источника на расстоянии , а от второго – на расстоянии .

 

 

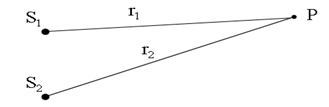
Рис.1. Два когерентных источника S₁ и S₂

 

Будем рассматривать только напряженности электрических полей световых волн, так как известно, что физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются именно электрическим полем световой волны.

Напряженность электрического поля световой волны называется световым вектором.

Световые векторы и  волн, приходящих в точку Р, имеют вид:

, (1)

, (2)

где – время; 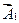, 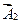- амплитуды световых векторов; – одинаковая для обеих волн частота; – волновое число, связанное с длиной волны  следующим образом: ;  и – начальные фазы. Согласно принципу суперпозиции при наложении двух волн образуется волна, световой вектор которой равен сумме световых векторов складываемых волн:

(3)

Будем считать, что колебания световых векторов в волнах, которые создают источники, происходят вдоль одного направления (т.е. волны плоскополяризованы в одной плоскости). Тогда векторная сумма (3) переходит в скалярную:

(4)

При сложении двух колебаний одинаковой частоты, происходящих вдоль одного направления, получаются колебание той же частоты, происходящее вдоль того же направления. Его амплитуду можно вычислить векторным методом сложения колебаний, который заключается в том, что каждому колебанию ставится в соответствие вектор (рис.2).  

 

 

 

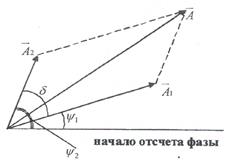
Рис. 2. Векторный метод сложения колебаний

 

Длины векторов 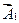 и в некотором масштабе равны амплитудам волн (1) и (2), а углы ψ₁ и ψ₂ между ними и началом отчета фазы равны:

ψ₁₌ φ₁ - kr₁, ψ₂₌ φ₂ – kr₂      (5)

Амплитуда  результирующей волны равна сумме векторов  и , и ее модуль находится по теореме косинусов:

, (6)

где δ =ψ₂ - ψ₁ называется разностью фаз волн.

Любой прибор, регистрирующий свет (в том числе глаз), реагирует на поток энергии, переносимый световой волной. Поток энергии пропорционален E² – квадрату светового вектора. Периоды T световых волн составляют порядка 10^-15 с. Приборы не могут уследить за такими быстрыми изменениями потока энергии и дают средний поток, пропорциональный A² – квадрату амплитуды светового вектора. Средний поток энергии называется интенсивностью световой волны и обозначается I.

Переходя от амплитуд к интенсивностям соотношение (6) можно переписать в виде:

(7)

Из (7) следует, что интенсивность результирующей волны не равна сумме интенсивностей перекрывающихся волн.

Таким образом, интерференция – это явление наложения волн, при котором не происходит простое сложение их интенсивностей.

Слагаемое , приводящее к отличию I от суммы I₁+ I₂, называется интерференционным членом.