3.1. Объяснение нового материала.
Определение 1. Последовательностей (yn) называют ограниченной сверху, если существует такое число М, что для любого n 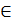 N выполняется неравенство
N выполняется неравенство 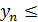 М.
М.
Определение 2. Последовательность (уn)называют ограниченной снизу, если существует такое число m, что для любого n 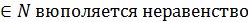
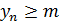 .
.
Если последовательность ограничена cверху и снизу, то ее называют ограниченной последовательностью.
Пример 1.
Дана числовая последовательность: 1, 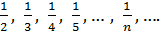 Определите, является ли она ограниченной?
Определите, является ли она ограниченной?
Решение. Максимальное значение, которое может принимать эта числовая последовательность это 1; а минимальное – 0. Значит эта числовая последовательность ограниченная.
Определение 3. Последовательность (yn) называют возрастающей, если каждый её элемент (кроме первого) больше предыдущего:
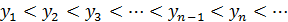
Пример 2. Возрастающая последовательность 2, 4, 6, 8, 10,....
.. Последовательность (yn) называют убывающей, если каждый её элемент (кроме первого) меньше предыдущего:
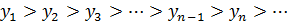
Пример 3.
Исследовать на ограниченность последовательность
yn= 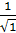 +
+ 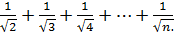
Решение.
y1= 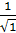 , y2=
, y2= 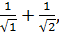 y3=
y3= 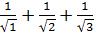 и т.д. Эта последовательность ограничена снизу. Наименьший элемент - этой последовательности y1=
и т.д. Эта последовательность ограничена снизу. Наименьший элемент - этой последовательности y1= 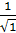 .
.
Ответ: последовательность ограничена снизу.
Возрастающие и убывающие последовательности объединяют общим термином –монотонные последовательности. Например, 1, 4, 9, 16, 25,...,n2 ,... и 1, 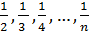 ...-многоточие последовательности, а последовательность 1,-
...-многоточие последовательности, а последовательность 1,- 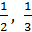 , -
, -  ,...,(-1)n-1
,...,(-1)n-1 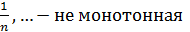
Если функция y = f(x) возрастает (убывает) на луче 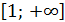 , то последовательность yn = f(n) – возрастающая (убывающая).
, то последовательность yn = f(n) – возрастающая (убывающая).
Пример 4. Исследовать на монотонность последовательность yn= 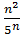 .
.
Решение.
Выпишем n-й и (n+1)-й члены последовательности: yn= 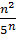 , yn+1=
, yn+1= 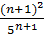 . Найдём их разность
. Найдём их разность
yn+1 - yn = 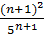 -
- 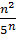 =
= 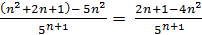 Для любых значений n yn+1 – yn, значит последовательность убывает.
Для любых значений n yn+1 – yn, значит последовательность убывает.
Урок
Числовая последовательность, способы ее задания, вычисление членов последовательности. Предел последовательности.
Практическая работа.
Рассмотрим две числовые последовательности - (yn), (xn).
(xn): 1, 3, 5, 7, 9, 11,...;
(yn): 1, 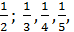 ...
...  ,....
,....
xn
0 1 3 5 7 9 11
yn
0 



Члены последовательности(yn) сгущаются около точки 0 - говорят, что эта последовательность сходится к точке 0. У последовательности (xn) такой точки сгущения нет – эта последовательность расходится.
Сходящаяся последовательность имеет предел.
Определение. Число b называют пределом последовательности (yn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.
В математике это обозначается так: yn b или так: 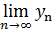 .
.
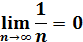
Пример 1. Найти предел последовательности  ,
, 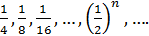
Решение. Последовательность сходится к 0.
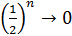 или
или 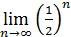 = 0.
= 0.
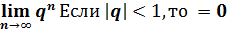 ,
, 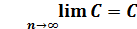
 2020-06-12
2020-06-12 160
160








