Геометрический смысл производной

Учащиеся повторяют определение в парах и вслух. Учитель демонстрирует фрагмент презентации о геометрическом смысле производной, проговаривают, что применяется практически при нахождении касательной к графику функции, решении задач на определение угла наклона касательной к графику функции, относительно положительного направления оси ОХ.

(слайды 7, 8)

Уравнение касательной к графику функции в общем виде записывается на доске (слайд 9).

Повторение алгоритма написания уравнения касательной к графику данной функции в точке с абсциссой . Двое учащихся у доски решают.

Задание 1. Напишите уравнение касательной к графику функции y = x  – 4 в точке с абсциссой = -2 (один учащийся решает у доски, остальные в тетрадях).

Решение:

1. Находим производную функции: у΄ = 2x

2. Находим значение производной функции в точке = -2: y’(-2) = - 4

3. Находим значение функции в точке  = -2: у(-2) = 0

4. Подставим в уравнение касательной найденные значения и получим ответ: у = -4х – 8

Задание 2. Найти, под каким углом ось ОХ пересекает параболу у=х² + х (один учащийся решает у доски, остальные в тетрадях).

Решение:

1. Найдем точки пересечения параболы с осью ОХ (у = 0): х² + х =0;

 х= 0, х= -1. Точки пересечения параболы с осью ОХ имеют координаты

 А(-1;0) и В(0;0);

2. Найдем угловые коэффициенты касательных к параболе в точках А и В:

а) производная функции равна у΄ = 2x + 1,

б) y΄ (-1) = -1=k₁, y΄ (0) = 1 = k₂,

3. Углы, образованные касательными в точках пересечения параболы с осью  ОХ: tg α₁=-1, α₁ = 135°; tg α₂= 1, α₂ = 45°.

Ответ: α₁= = 135°, α₂= 45°.

Задание 3. ( дифференцированная самостоятельная работа учащихся)

(слайд 10):

а) Дана функция у(x) = x² – 2х. Напишите уравнение касательной к графику этой функции в точке с абсциссой 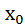 = 2.

б) Дана функция у(x) = Напишите уравнение касательной к графику этой функции в точке с абсциссой  = - 4.

в) Дана функция у(x) = sin 2x. Напишите уравнения касательных к графику этой функции в точках с абсциссами 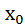 = 0 и = π / 2.

Первый пример оценивается “1 б”, второй– “2 б”, третий– “3б”. Решение в тетрадях с последующей взаимопроверкой.

Ответы проверяются (слайд 11) и выставляются баллы /взаимооценка /:

а) у = 2х – 4,

б) у = - 1,5х - 9,

в) у = 2х и у = -2х + π.