Обозначим количество изделий, выпускаемых из i-го филиала в j-ый пункт потребления через 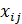 .
.
Проверка сбалансирования задачи
Проверим равенство суммарного изготовления изделий и суммарного спроса
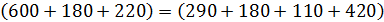
Откуда следует - задача сбалансирована, поскольку спрос изделий равен объему изготовления изделий.
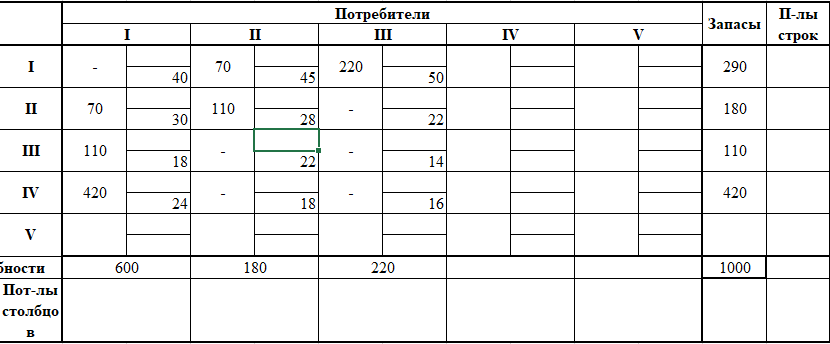
Согласно результатам проверки сбалансированности задачи, в транспортной матрице должно быть 4 строки, которые соответствуют филиалам и 4 столбца, которые соответствуют центрам распределения.
Транспортная матрица задачи №19*
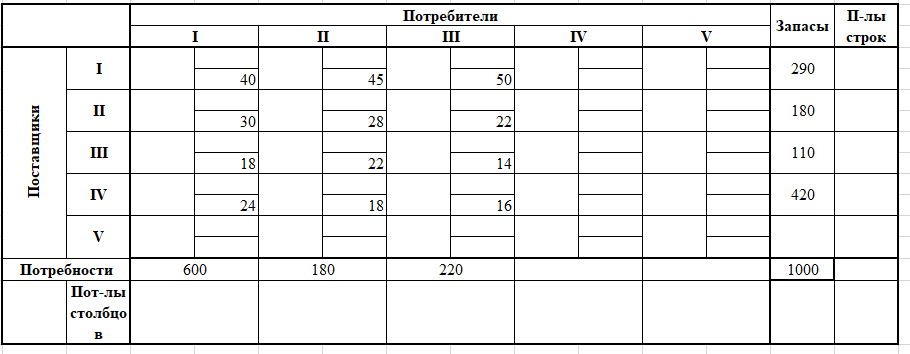
Задание ЦФ
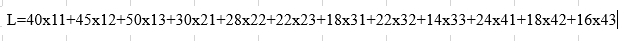
Задание ограничений:
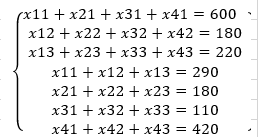
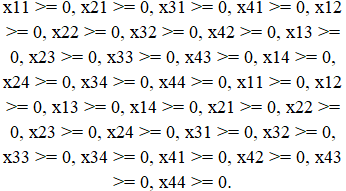
Цель:
1. Отработать и закрепить умения строить опорный план транспортной задачи двумя методами: методом северо-западного угла и методом наименьшей стоимости.
2. Отработать и закрепить умение находить оптимальное решение транспортной задачи методом потенциалов.

Решение:
1. Построим план двумя методами: методом северо-западного угла и методом наименьшей стоимости, и выберем тот план, который будет наилучшим, то есть получим минимальные затраты на перевозку однородного груза.
А) Строим начальный план методом северо-западного угла. Составим таблицу значений:
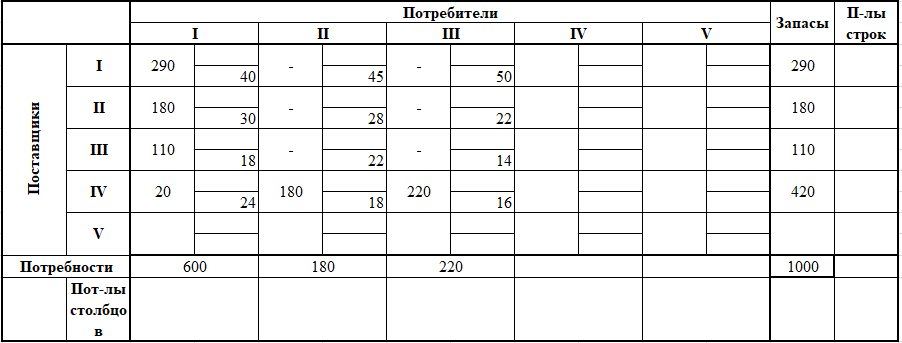
начальный план
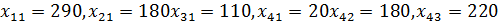
невыраженный.
При таком плане суммарные транспортные издержки равны:
Б) Строим начальный план методом наименьшей стоимости. Составим таблицу значений:
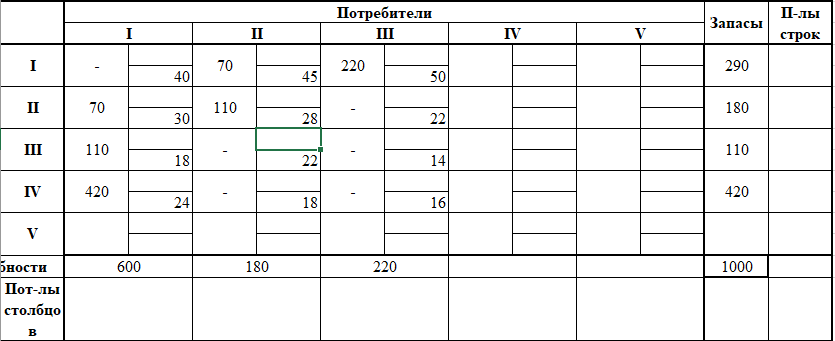
Начальный план:
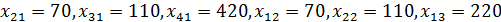
При таком плане транспортные издержки
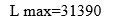
Сравнивая транспортные издержки, видим, что план, построенный методом наименьшей стоимости, лучший.
2. Выбираем лучший план и находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана: 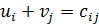
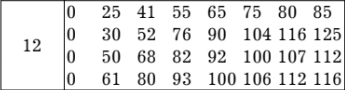
Производственное объединение состоит из 4 предприятий (n = 4). Общая сумма капитальных вложений равна 700 млн. руб. (b = 700), выделяемые предприятием суммы кратны 100 млн. руб. Если j-е предприятие получает инвестиции в объеме Е млн. руб. в год, то прирост годовой прибыли на этом предприятии составит 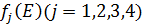 . Значения этих функций
. Значения этих функций 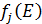 известны и для каждого варианта записаны в таблице ниже в след. виде:
известны и для каждого варианта записаны в таблице ниже в след. виде:
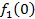
| 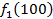
| 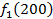
| 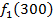
| 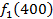
| 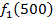
| 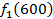
| 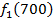
|
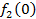
| 
| 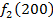
| 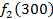
| 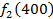
| 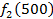
| 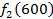
| 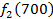
|
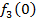
| 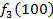
| 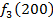
| 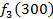
| 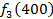
| 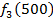
| 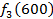
| 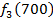
|
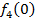
| 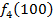
| 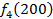
| 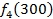
| 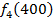
| 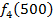
| 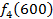
| 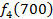
|
Требуется найти такое распределение инвестиций между предприятиями, которое максимизирует суммарный прирост прибыли на всех предприятиях вместе. Для этого необходимо составить математическую модель динамической задачи распределения инвестиций и решить ее методом динамического программирования, основывая каждый шаг вычислительного процесса.
Решение:
Составим математическую модель динамической задачи распределения инвестиций и решим ее методом динамического программирования. В качестве шага управления примем вложение инвестиций в одно предприятие. Количество шагов равно количеству предприятий. Рассмотрим алгоритм с конца. Предположим на последнем шаге мы распределяем средства в четвертое предприятие. Зависимость прироста прибыли 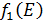 от объема вложений Е на четвертом предприятии определяется верхней строкой таблицы исходных данных.
от объема вложений Е на четвертом предприятии определяется верхней строкой таблицы исходных данных.
Рассмотрим предпоследний шаг задачи. На данном шаге нам необходимо рассмотреть суммарный прирост прибыли на двух предприятиях от совместного вложения инвестиций в них, пусть это будут предприятия 4 и 3. Необходимо найти условный оптимальный прирост прибыли на этих двух предприятиях, при условии вложения определенной суммы инвестиций в оба предприятия. Заполним таблицу, в верхнюю строку которой выпишем значения прироста прибыли четвертого предприятия от объема инвестиций - 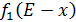 . В левый столбец выпишем значения
. В левый столбец выпишем значения 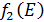 - прироста прибыли третьего предприятия от объема инвестиций.
- прироста прибыли третьего предприятия от объема инвестиций.
Значения 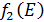 складываем со значениями
складываем со значениями 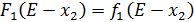 , и заносим в таблицу. Каждая северо-восточная диагональ этой таблицы определяет возможные значения суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между двумя предприятиями. На каждой северо-восточной диагонали находим наибольшее число (которое выделяем жирным).
, и заносим в таблицу. Каждая северо-восточная диагональ этой таблицы определяет возможные значения суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между двумя предприятиями. На каждой северо-восточной диагонали находим наибольшее число (которое выделяем жирным).
(Табл. 1)
| x3 | E - x3 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F3(x3)/F4(E - x4) | 0 | 61 | 80 | 93 | 100 | 106 | 112 | 116 | |
| 0 | 0 | 0 | 61 | 80 | 93 | 100 | 106 | 112 | 116 |
| 100 | 50 | 50 | 111 | 130 | 143 | 150 | 156 | 162 |
|
| 200 | 68 | 68 | 129 | 148 | 161 | 168 | 174 |
|
|
| 300 | 82 | 82 | 143 | 162 | 175 | 182 |
|
|
|
| 400 | 92 | 92 | 153 | 172 | 185 |
|
|
|
|
| 500 | 100 | 100 | 161 | 180 |
|
|
|
|
|
| 600 | 107 | 107 | 168 |
|
|
|
|
|
|
| 700 | 112 | 112 |
|
|
|
|
|
|
|
Составим таблицу 2:
· В верхнюю строку выпишем возможный объем инвестиций, выделяемый на 2 предприятия: Е.
· Во вторую строку запишем условно оптимальное значение суммарного прироста прибыли на двух предприятиях - 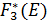 соответствующее объему инвестиций из строки 1.
соответствующее объему инвестиций из строки 1.
· Третью строку заполним значениями 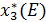 – объем инвестиций, приходящийся на второе предприятие.
– объем инвестиций, приходящийся на второе предприятие.
(Табл. 2)
| E | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F3*(E) | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 |
| X3*(E) | 0 | 0 | 100 | 100 | 200 | 300 | 300 | 400 |
Рассмотрим предыдущий шаг, на котором изучим возможный прирост прибыли на трех предприятиях от совместного вложения объема инвестиций Е в них, пусть это будут предприятия 4,3 и 2, и найдем оптимальный вариант их распределения. Для этого в верхнюю строку выпишем значения условно оптимального прироста прибыли от объема инвестиций - 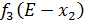 , вложенных в предприятии 4 и3 из таблицы 2. В левый столбец выпишем значения
, вложенных в предприятии 4 и3 из таблицы 2. В левый столбец выпишем значения 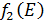 – прироста прибыли второго предприятия от объема инвестиций. Заполним ячейки таблицы значениями суммы этих величин.
– прироста прибыли второго предприятия от объема инвестиций. Заполним ячейки таблицы значениями суммы этих величин.
Как и на предыдущем шаге найдем максимальное значение суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между предприятиями.
(Табл. 3)
| x2 | E - x2 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F2(x2)/F3(E - x2) | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 | |
| 0 | 0 | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 |
| 100 | 30 | 30 | 91 | 141 | 160 | 178 | 192 | 205 |
|
| 200 | 52 | 52 | 113 | 163 | 182 | 200 | 214 |
|
|
| 300 | 76 | 76 | 137 | 187 | 206 | 224 |
|
|
|
| 400 | 90 | 90 | 151 | 201 | 220 |
|
|
|
|
| 500 | 104 | 104 | 165 | 215 |
|
|
|
|
|
| 600 | 116 | 116 | 177 |
|
|
|
|
|
|
| 700 | 125 | 125 |
|
|
|
|
|
|
|
По данным таблицы 3 составим таблицу 4, в которой:
· В верхнюю строку выпишем возможный объем инвестиций, выделяемый на три предприятия: Е.
· Во вторую строку запишем условно оптимальное значение суммарного прироста прибыли на двух предприятиях - 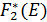 соответствующее объему инвестиций из строки 1.
соответствующее объему инвестиций из строки 1.
· Третью строку заполним значениями 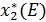 – объем инвестиций, приходящийся на второе предприятие.
– объем инвестиций, приходящийся на второе предприятие.
(Табл. 4)
| E | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F2*(Е) | 0 | 61 | 111 | 141 | 163 | 187 | 206 | 224 |
| X2*(E) | 0 | 0 | 0 | 100 | 200 | 300 | 300 | 300 |
Так как по условию задачи вложения инвестиций осуществляются в 4 предприятия, то переходим к последнему этап поиска условно оптимального вложения средств, рассмотрев вложения в четыре предприятия. Для этого составим таблицу аналогично 3. В верхнюю строку таблицы 5 выпишем значения условно оптимального прироста прибыли от объема инвестиций - 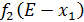 , вложенных в предприятия 4,3 и 2 из таблицы 4. В левый столбец выпишем значения
, вложенных в предприятия 4,3 и 2 из таблицы 4. В левый столбец выпишем значения 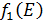 – прироста прибыли четвертого предприятия от объема инвестиций.
– прироста прибыли четвертого предприятия от объема инвестиций.
Так как по условию задачи в четыре предприятии вкладывается полный объем имеющихся средств, то в таблицу 5 мы заполним ячейки только на диагонали, соответствующей объему инвестиций Е = 700 млн. руб. заполним эти ячейки значениями сумм величин 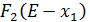 и
и 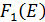 . на этой диагонали найдем максимальное значение, соответствующее оптимальному плану размещения инвестиций по четырем предприятиям.
. на этой диагонали найдем максимальное значение, соответствующее оптимальному плану размещения инвестиций по четырем предприятиям.
(Табл. 5)
| x1 | E - x1 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F1(x1)/F2(E - x1) | 0 | 61 | 111 | 141 | 163 | 187 | 206 | 224 | |
| 0 | 0 |
|
|
|
|
|
|
| 224 |
| 100 | 25 |
|
|
|
|
|
| 231 |
|
| 200 | 41 |
|
|
|
|
| 228 |
|
|
| 300 | 55 |
|
|
|
| 218 |
|
|
|
| 400 | 65 |
|
|
| 206 |
|
|
|
|
| 500 | 75 |
|
| 186 |
|
|
|
|
|
| 600 | 80 |
| 141 |
|
|
|
|
|
|
| 700 | 85 | 85 |
|
|
|
|
|
|
|
В таблице 5 наибольшее значение на диагонали для значения Е = 700 равно 231, таким образом максимальное значения суммарного прироста прибыли на всех предприятиях вместе, будет:
Zmax = 231 млн. руб.
Определим, при каком распределении вложенных средств по четырем предприятиям достигается это максимальное значение суммарного прироста прибыли. Рассмотрим шаги задачи и таблицы на этих шагах в обратном порядке.
Из таблицы 5 видно, что Zmax достигается при выделении первому предприятию инвестиций в размере 100 млн. руб., таким образом, в оптимальном решении:
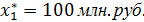
На долю остальных трех предприятий остается 600 млн. руб. Из таблицы 4 определим оптимальное распределение инвестиций в размере Е = 600 млн. руб. и долю этих инвестиций, приходящуюся на второе предприятие.
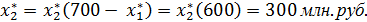
Таким образом, для обеспечения оптимального решения второе предприятие должно получить инвестиции в размере
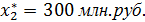 При этом размер инвестиций, приходящийся на предприятия 4 и 3, составит Е = 300 млн. руб. Продолжая обратный процесс, переходим к таблице 2 и найдем оптимальное распределение этих средств между предприятиями 4 и 3.
При этом размер инвестиций, приходящийся на предприятия 4 и 3, составит Е = 300 млн. руб. Продолжая обратный процесс, переходим к таблице 2 и найдем оптимальное распределение этих средств между предприятиями 4 и 3.
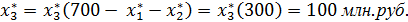
Оптимальный размер инвестиций, которых должно получить третье предприятие составляет 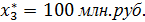 На долю четвертого предприятия, при этом остается:
На долю четвертого предприятия, при этом остается:
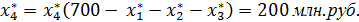
Проверим по данным исходной таблицы выполнение равенства:
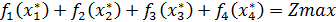
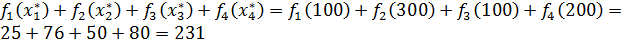 , равенство выполняется.
, равенство выполняется.
Ответ:
Наилучшим является следующее распределение капитальных вложений по предприятиям:
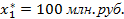 ,
, 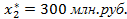 ,
, 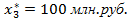 ,
, 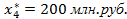
Оно обеспечивает производственному объединению наибольший возможный прирост прибыли Zmax = 231 млн. руб.
Пр.10 «Нахождение кратчайших путей в графе. Алгоритм Дейкстры»
Цель:
Приобретение навыков нахождения кратчайших путей в графе с помощью алгоритма Дейкстры.
Вариант 10.

Изобразим граф с указанием числовых значений весов дуг и направлением ориентации рёбер. 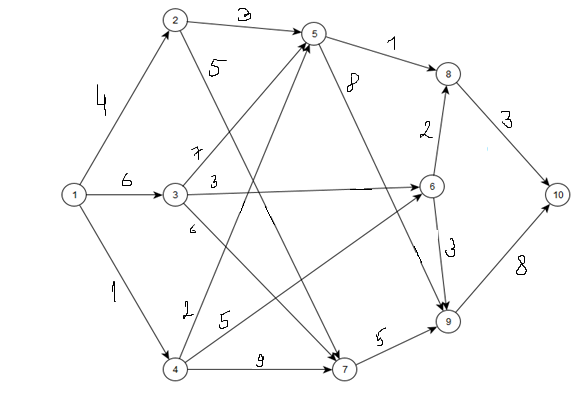 С помощью алгоритма Дейкстры найдем длины наименьших путей, а также массив вершин предшественников на путях, из источника I – вершины 1 до каждой другой вершины графа, а также до стока – вершины 10.
С помощью алгоритма Дейкстры найдем длины наименьших путей, а также массив вершин предшественников на путях, из источника I – вершины 1 до каждой другой вершины графа, а также до стока – вершины 10.
Для этого нам понадобиться выполнить 9 итераций алгоритма
Вершины, включенные в S на каждом шаге, будем помечать желтым цветом (рис. 1), пути до вершин, которые возможно определить на текущем шаге алгоритма – зеленым, путь минимальной длинны на данном шаге – красным. Недоступные пути – синим.
Шаг 1.
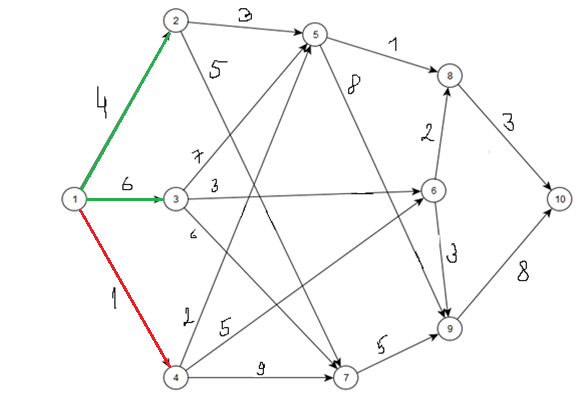

Табл. 1.
Шаг 2.
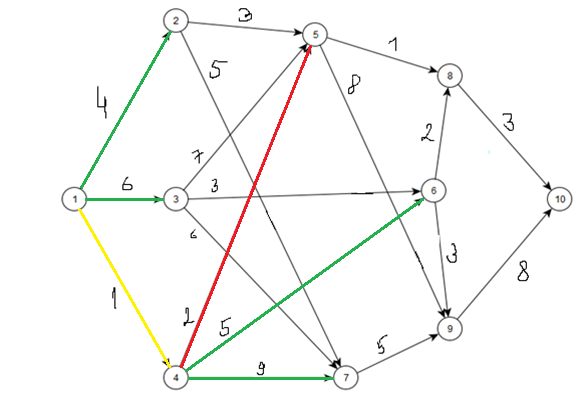

Табл. 2.
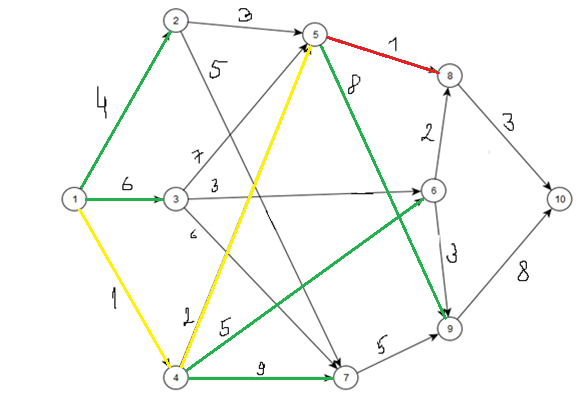

Табл. 3.
Шаг 4.
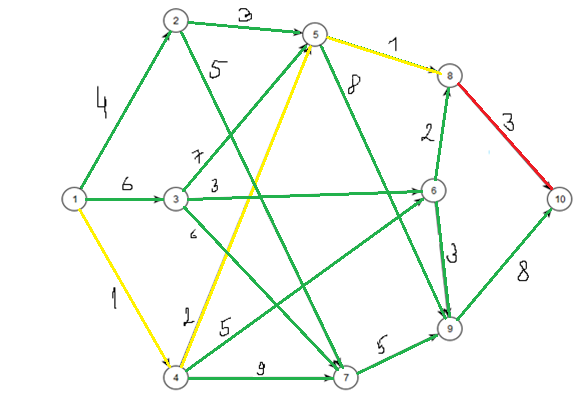
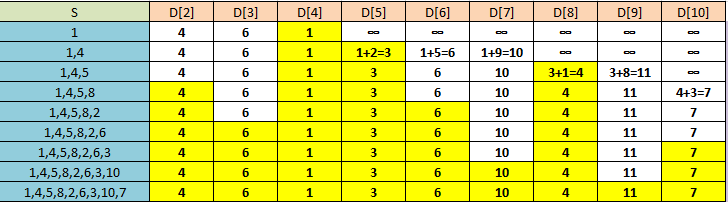
Табл. 4.
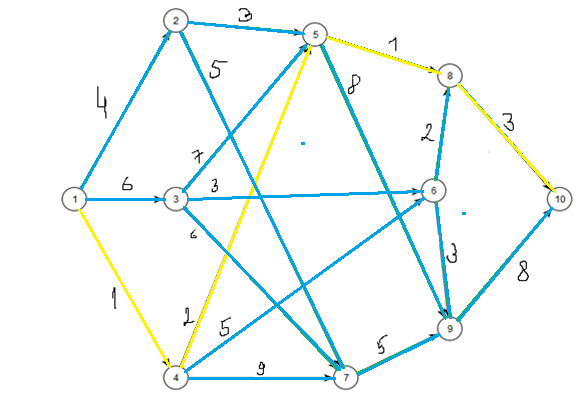

Кратчайший путь пути от источника – вершины 1 до стока – вершины 10 будет равен: D[10] = 7 проходит через вершины 1 -> 4 -> 5 -> 8 -> S
 2020-06-12
2020-06-12 190
190








