Трехмерное уравнение Лапласа

    Задача 1. Найти стационарное распределение тепла в параллелепипеде 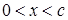, 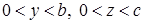. Температура на грани  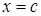равна 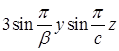, на остальных гранях температура равна нулю.

    Решение. Решение 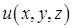 уравнения Лапласа

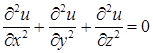                                        (1)

с краевыми условиями

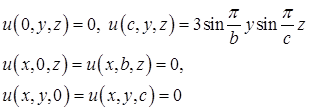                  (2)

будем искать в виде

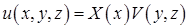.                               (3)

Это представление подсказывают краевые условия, неоднородные только по .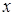

Подставим функцию 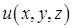 в уравнение:

.

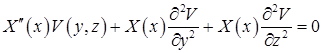Переменные разделяются:

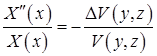.                                      (4)

Краевые условия по 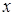 приводят к соотношениям

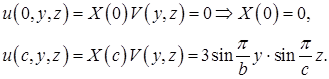
Значит, если принять 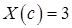, то остается

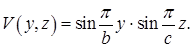                                         (5)

Заметим, что функция (5) удовлетворяет нулевым краевым условиям:

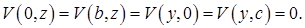
Обращаем внимание на то, что для функции 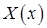 краевые условия ненулевые, то есть для этой функции мы не получили задачу Штурма – Лиувилля.

В соотношении (4) левая часть зависит только от 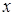, а правая часть – от 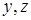. Равенство этих частей возможно лишь при условии

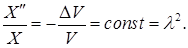                                          (5)

    Рассмотрим уравнение

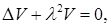                                                (6)

решение которого 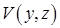 нам известно:  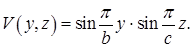 Заметим, что только при положительных значениях константы, фигурирующей в соотношении (5), уравнение (6) может иметь решение вида (5). Найдем значения 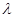, при которых уравнение (6) удовлетворяется функцией (5).

    Вычислим производные

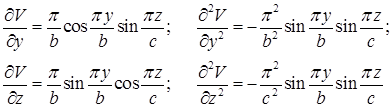
и подставим их в уравнение (6)

.

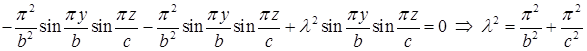    Осталось найти функцию 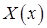, удовлетворяющую уравнению

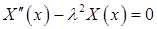                                                (7)

и неоднородным краевым условиям

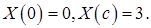                                                 (8)

    Запишем общее решение уравнения (7):

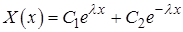
    Из краевых условий получаем

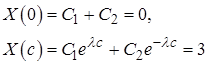
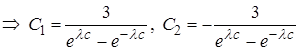
    Значит, решение задачи (7) - (8) имеет вид

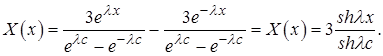            (9)

Осталось подставить найденную функцию (9) и функцию (5) в представление (3):

                 

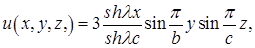
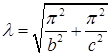
    Легко проверить, что полученная функция действительно удовлетворяет и уравнению (1), и краевым условиям (2). ●