Свойства преобразований Фурье

Формулы прямого и обратного преобразования Фурье позволяют по сигналу s(t) определить его спектральную плотность S(jω) и, если в этом есть необходимость, по известной спектральной плотности S(jω) определить сигнал s(t). Для обозначения этого соответствия между сигналом и его спектром применяется символ s(t)↔ S(jω).

С помощью свойств преобразований Фурье можно определить спектр измененного сигнала, преобразуя спектр первоначального сигнала.

Основные свойства:

1. Линейность

 

s₁(t)↔ S₁(jω)

⁞         ⁞

s_n(t)↔ S_n(jω)

___________________________

 

Воспользуемся прямым преобразованием Фурье

 

 

Окончательный результат

 

                 

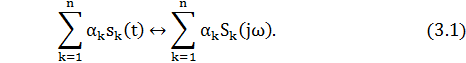
Вывод: прямое преобразование Фурье, является линейной операцией, обладает свойствами однородности и аддитивности. Поэтому спектр суммы сигналов равен сумме спектров.

2. Спектр сигнала, сдвинутого во времени

 

s(t)↔ S(jω)

____________

s(t±t₀)↔S_c(jω).

 

 

Окончательный результат

 

                                 (3.2)

 

Вывод: сдвиг сигнала во времени на величину ±t₀ приводит к изменению фазовой характеристики спектра на величину ±ωt₀. Амплитудный спектр не изменяется.

3. Изменение масштаба во времени

 

s(t)↔ S(jω)

___________________________

s(αt)↔ S_м(jω).

 

 

 

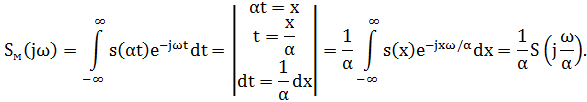
Окончательный результат

 

 

Вывод: при сжатии (расширении) сигнала во времени в определенное число во столько же раз расширяется (сжимается) его спектр по оси частот при пропорциональном уменьшении (увеличении) амплитуд его составляющих.

4. Спектр производной

 

s(t)↔ S(jω)

___________________________

ds(t)/dt↔ S_п(jω).

 

Для определения спектра производной сигнала возьмем производную по времени от правой и левой части обратного преобразования Фурье:

 

 

Окончательный результат

 

                                  

Вывод: спектр производной сигнала равен спектру исходного сигнала, умноженному на jω. При этом амплитудный спектр изменяется пропорционально изменению частоты, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2 при ω>0 и равная -π/2 при ω<0.

5. Спектр интеграла

 

s(t)↔ S(jω)

___________________________

 

Возьмем интеграл от правой и левой части обратного преобразования Фурье

 

 

Сравнивая результат с обратным преобразованием Фурье, получаем

 

                                     

Окончательный результат

 

                                  

Вывод: спектр сигнала, равного интегралу от исходного сигнала, равен спектру исходного сигнала, деленному на jω. При этом амплитудный спектр изменяется обратно пропорционально изменению частоты, а к фазовой характеристике исходного сигнала добавляется постоянная составляющая, равная π/2 при ω<0 и равная -π/2 при ω>0.

6. Спектр произведения двух сигналов

 

s₁(t)↔ S₁(jω)

s₂(t)↔ S₂(jω)

___________________________

s₁(t) s₂(t)↔ S_пр(jω).

 

Найдем спектр произведения двух сигналов с помощью обратного преобразования Фурье

 

 

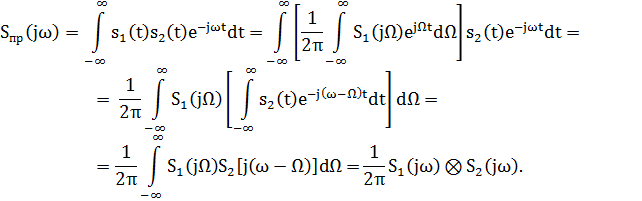
Окончательный результат

 

               

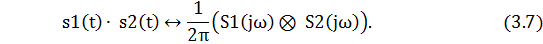
Вывод: Спектр произведения двух сигналов равен свертке их спектров, умноженной на коэффициент 1/(2π).

7.  Свойство дуальности

Если сигналу s(t) соответствует амплитудный спектр S(ω), то сигналу, имеющему форму такую же, как форма амплитудного спектра S(ω), соответствует спектр, имеющий форму сигнала s(t).

8. Смещение спектра сигнала

 

s_в(t)↔ S_в(jω)

___________________________

s_р(t)=s_в(t)cos(ω₀t)↔S_р(jω).

 

Произведение двух сигналов s₁(t) и s₂(t)= cos(ω₀t+ φ) образует гармонический сигнал s(t)= s₁(t)cos(ω₀t+ φ). Так если s₁(t) – видеоимпульс, то s(t) – это радиоимпульс с несущей частотой ω₀.

Определим спектральную плотность сигнала s(t):

 

 

Таким образом, спектральная плотность сигнала s_р(t) равна

 

 

Вывод: При умножении сигнала на гармоническую функцию образуется сигнал, спектр которого представляет собой преобразованный спектр сигнала s₁(t). Суть преобразования заключается в переносе спектра на ±ω₀ с уменьшением вдвое его величины.

Рассмотренные свойства преобразования Фурье значительно облегчают вычисление спектров различных сигналов.